
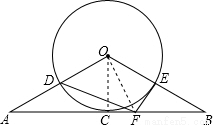
如图,AB经过⊙O上的点C,且OA=OB,CA=CB,⊙O分别与OA、OB的交点D、E恰好是OA、OB的中点,EF切⊙O于点E,交AB于点F.
(1)求证:AB是⊙O的切线;
(2)若∠A=30°,⊙O的半径为2,求DF的长.

(1)证明见解析;(2)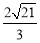 .
.
【解析】
试题分析:(1)利用等腰三角形的性质以及切线的判定进而得出即可.
(2)利用等腰三角形的性质得出∠FOE=∠B=30°,进而得出FO的长,再利用勾股定理得出DF的长即可.
试题解析:(1)如图,连接CO,
∵AO=BO,CA=CB,∴CO⊥AB.
∵CO为⊙O的半径,∴AB是⊙O的切线.
(2)如图,连接FO,
∵OA=OB,∠A=30°,OC⊥AB,CO=2,∴AO=4,∠B=30°.
∵⊙O分别与OA、OB的交点D、E恰好是OA、OB的中点,EF切⊙O于点E,
∴FE⊥BO,OE=BE=2. ∴FO=FB. ∴∠FOE=∠B=30°.
∴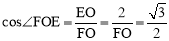 ,解得:
,解得: .
.
∵∠A=∠B=∠BOF=30°,∴∠AOF=90°.
∴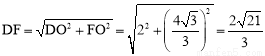 .
.
考点:1.切线的判定和性质;2等腰三角形的性质;3.勾股定理.


科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,抛物线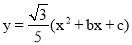 过点
过点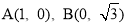 ,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且?CPD=
,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且?CPD= .
.
(1)求抛物线的解析式;
(2)若点P的横坐标为m,△PCD的面积为S,求S与m之间的函数关系式;
(3)过点P作PE⊥DP,连接DE,F为DE的中点,试求线段BF的最小值.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
如图,已知边长为4的正方形ABCD, E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
2014年5月4日,在“百度搜索”的“手机型号排行榜”中显示,排名第一位的是苹果 iphone5S,关注指数为46590,将46590用科学记数法表示为( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江龙东卷)数学(解析版) 题型:选择题
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )
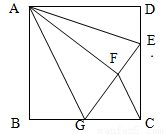
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com