
如图,在平面直角坐标系xOy中,抛物线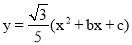 过点
过点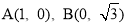 ,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且?CPD=
,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且?CPD= .
.
(1)求抛物线的解析式;
(2)若点P的横坐标为m,△PCD的面积为S,求S与m之间的函数关系式;
(3)过点P作PE⊥DP,连接DE,F为DE的中点,试求线段BF的最小值.

(1) ;(2)
;(2) (m<3);(3)
(m<3);(3) .
.
【解析】
试题分析:(1)由抛物线 过点
过点 ,根据点在曲线上点的坐标满足方程的关系,应用待定系数法求解即可.
,根据点在曲线上点的坐标满足方程的关系,应用待定系数法求解即可.
(2)证明△PCD是等边三角形,用m表示CP和PG,由 即可求得S与m之间的函数关系式.
即可求得S与m之间的函数关系式.
(3)通过证明△CPF≌△CDF得∠PCF=∠DCF,根据垂直线段最短的性质知线段BF 的最小值为点B到直线CF的距离.
(1)依题意,得 ,解得
,解得  .
.
∴抛物线的解析式为 ,即
,即 .
.
(2)∵ ,∴抛物线的对称轴为
,∴抛物线的对称轴为 .∴C(3,0).
.∴C(3,0).
∵ ,∴
,∴ .∴
.∴ .
.
∴∠OCB= .∴∠PCD=
.∴∠PCD= .
.
∵∠CPD= ,∴∠CDP=
,∴∠CDP= .∴△PCD是等边三角形.
.∴△PCD是等边三角形.
如图,过点P作PQ⊥x轴于点Q,PG∥x轴,交CD于点G ,
∵点P的横坐标为m,∴OQ=m,CQ=3-m.
∴ ,PG=CQ=3-m.
,PG=CQ=3-m.
∴ ,即
,即 (m<3).
(m<3).

(3)如图,连接PF、CF.
∵PE⊥DP,F为DE的中点,∴PF= =DF.
=DF.
∵CP=CD,CF=CF,∴ △CPF≌△CDF.∴∠PCF=∠DCF.
∴点F在∠PCD的平分线所在的直线上.
∴BF的最小值为点B到直线CF的距离.
∵∠OCB=∠BCF= ,∴点B到直线CF的距离等于OB.
,∴点B到直线CF的距离等于OB.
∴BF的最小值为 .
.

考点:1.动点问题;2.二次函数综合题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.锐角三角函数定义;6.特殊角的三角函数值;7.等边三角形的判定和性质;8.直角三角形斜边上中线的性质;9.全等三角形的判定和性质;10.垂直线段的性质.


科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:选择题
如表是我市11个区县去年5月1日最高气温(℃)的统计结果:
市中区 | 峨眉山市 | 沙湾区 | 五通桥区 | 金口河区 | 犍为县 | 井研县 | 夹江县 | 沐川县 | 峨边县 | 马边县 |
26 | 25 | 29 | 26 | 28 | 26 | 26 | 27 | 25 | 28 | 25 |
该日最高气温的众数和中位数分别是( ).
A.25℃,26℃ B.26℃,26℃
C.25℃,25℃ D.26℃,27℃
查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:填空题
如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O上,若⊙O的半径为5,AB=4,则AD边的长为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:选择题
不等式组 的解集是( )
的解集是( )
A.﹣1<x≤1 B.﹣1<x<1 C.x>﹣1 D.x≤1
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:解答题
保障房建设是民心工程,某市从2009年加快保障房建设工程.现统计了该市从2009年到2013年这5年新建保障房情况,绘制成如图1、2所示的折线统计图和不完整的条形统计图.

(1)小颖看了统计图后说:“该市2012年新建保障房的套数比2011年少了.”你认为小颖的说法正确吗?请说明理由;
(2)求2012年新建保障房的套数,并补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考一模数学试卷(解析版) 题型:解答题
如图,AB经过⊙O上的点C,且OA=OB,CA=CB,⊙O分别与OA、OB的交点D、E恰好是OA、OB的中点,EF切⊙O于点E,交AB于点F.
(1)求证:AB是⊙O的切线;
(2)若∠A=30°,⊙O的半径为2,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com