
 ,0),直线
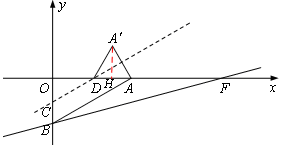
,0),直线 与x轴交于点F,与y轴交于点B,直线l∥AB且交y轴于点C,交x轴于点D,点A关于直线l的对称点为A′,连接AA′、A′D.直线l从AB出发,以每秒1个单位的速度沿y轴正方向向上平移,设移动时间为t.
与x轴交于点F,与y轴交于点B,直线l∥AB且交y轴于点C,交x轴于点D,点A关于直线l的对称点为A′,连接AA′、A′D.直线l从AB出发,以每秒1个单位的速度沿y轴正方向向上平移,设移动时间为t.
 于点E,以点C为圆心CE为半径作⊙C,求当t为何值时,⊙C与△AA′D三边所在直线相切?
于点E,以点C为圆心CE为半径作⊙C,求当t为何值时,⊙C与△AA′D三边所在直线相切? ;(2)证明见解析;(3)1或
;(2)证明见解析;(3)1或 .
. ,0),求出∠ODC=∠OAB=30°,由点A关于直线l的对称点为A',求出A'点的坐标(用t的代数式表示);(2)通过点F的坐标,得出AF,在Rt△OAB中,OA=
,0),求出∠ODC=∠OAB=30°,由点A关于直线l的对称点为A',求出A'点的坐标(用t的代数式表示);(2)通过点F的坐标,得出AF,在Rt△OAB中,OA= ,OB=2,求出AB,得AB=AF;(3)先由直线l是点A和A'的对称轴得直线l是∠A'DA的平分线,即得点C到直线AD和A'D的距离相等,当⊙C与AD相切时,也一定与A'D相切,通过直角三角形求解.
,OB=2,求出AB,得AB=AF;(3)先由直线l是点A和A'的对称轴得直线l是∠A'DA的平分线,即得点C到直线AD和A'D的距离相等,当⊙C与AD相切时,也一定与A'D相切,通过直角三角形求解. 与y轴交于点B,∴B(0,
与y轴交于点B,∴B(0, ).
). ,0),∴
,0),∴ . ∴∠ODC=∠OAB=30°.
. ∴∠ODC=∠OAB=30°. t. ∴OD=
t. ∴OD= . ∴AD=
. ∴AD= .
. ,∠A'DA="60°." ∴△A'DA是等边三角形.
,∠A'DA="60°." ∴△A'DA是等边三角形. ,A'H=
,A'H= .
. .
.
 与x轴交于点F ,∴F
与x轴交于点F ,∴F .
. ,0),∴AF=4.
,0),∴AF=4. ,OB=2,∴AB=4.
,OB=2,∴AB=4. CD,在Rt△OCD中,∠ODC=30°,OC=t
CD,在Rt△OCD中,∠ODC=30°,OC=t 2,∴CD=2t
2,∴CD=2t 4.
4. ,解得t=
,解得t= .
. 时,⊙C与△AA′D三边所在直线相切.
时,⊙C与△AA′D三边所在直线相切.


科目:初中数学 来源:不详 题型:解答题
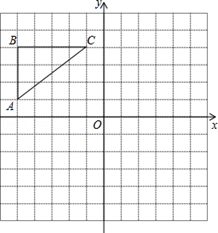
 的长是 (保留π).
的长是 (保留π).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 所在圆的圆心为
所在圆的圆心为 ,半径
,半径 为3米.
为3米.
 的度数;
的度数;
 取3.14)
取3.14)查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
 B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com