练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将一副三角板如图摆放，∠OAB=∠OCD=90°，∠AOB=60°，∠COD=45°，OM平分∠AOD，ON平分∠COB，则∠MON的度数为（ ）

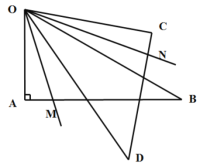
    A.60°B.45°C.65.5°D.52.5°

    【答案】D

    【解析】

    设∠AOM=∠DOM=x，∠CON=∠BON=y，则∠BOD=60-2x，根据∠AOB=60°，∠COD=45°，列出算式，求出x-y的度数，最后根据∠MON与各角之间的关系，即可求出答案．

    设∠AOM=∠DOM=x，∠CON=∠BON=y，则∠BOD=60°-2x

    ∵∠COD=45°

    ∴60°-2x+2y=45°，

    ∴x-y=7.5°

    ∴∠MON=x+(60°-2x)+y=60°(x-y）=52.5°

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小云想用7天的时间背诵若干首诗词，背诵计划如下：

    ①将诗词分成4组，第i组有首，i =1，2，3，4；

    ②对于第i组诗词，第i天背诵第一遍，第（）天背诵第二遍，第（）天背诵第三遍，三遍后完成背诵，其它天无需背诵，1，2，3，4；

    第1天

    第2天

    第3天

    第4天

    第5天

    第6天

    第7天

    第1组

    第2组

    第3组

    第4组

    ③每天最多背诵14首，最少背诵4首．

    解答下列问题：

    （1）填入补全上表；

    （2）若，，，则的所有可能取值为______；

    （3）7天后，小云背诵的诗词最多为______首．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系内，正方形ABCD中的顶点B，D的坐标分别是（0，0），（2，0），且A，C两点关于x轴对称，则C点对应的坐标是（ ）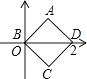

    A.（1，1）
    B.（1，﹣1）
    C.（1，﹣2）
    D.（2，﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形ABCD的边长为10厘米，点E在边AB上，且AE=4厘米，如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．设运动时间为t秒．

    （1）若点Q的运动速度与点P的运动速度相等，经过2秒后，△BPE与△CQP是否全等？请说明理由；

    （2）若点Q的运动速度与点P的运动速度不相等，则当t为何值时，能够使△BPE与△CQP全等；此时点Q的运动速度为多少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知下列命题:①若则②若则③对顶角相等；④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是（ ）

    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠BAC＝90°，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交射线BC于点F．（友情提醒：翻折前后的两个三角形的对应边相等，对应角相等．）

    　

    （1）如图①，当AE⊥BC时，求证：DE∥AC．

    （2）若，∠BAD＝x° ．

    ①如图②，当DE⊥BC时，求x的值；

    ②是否存在这样的x的值，使得△DEF中有两个角相等．若存在，并求x的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某家电商场计划用9万元从生产厂家购进50台电视机，已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．

    （1）若家电商场同时购进两种不同型号的电视机共50台，用去9万元，请你计算一下商场有哪几种进货方案？

    （2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，应选择哪种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)发现问题:如图①平行四边形AB、CD的对角线相交于点O,DE∥AC,CE∥BD，可知:四边形OCED是什么形(不需要证明).

    (2)类比探究:如图②矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD，四边形OCED是什么形,请说明理由；

    (3)拓展应用:如图③,菱形ABCD的对角线相交于点O,∠ABC=60°,BC=4,DE∥AC交BC的延长线于点F,CE∥BD求四边形ABFD的周长.

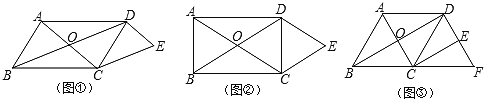
    查看答案和解析>>

    科目：初中数学 来源： 题型：

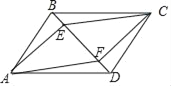
    【题目】如图，在ABCD中，经过A，C两点分别作AE⊥BD，CF⊥BD，E，F为垂足．

    （1）求证：△AED≌△CFB；

    （2）求证：四边形AFCE是平行四边形

    查看答案和解析>>

    同步练习册答案