
【题目】在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20. 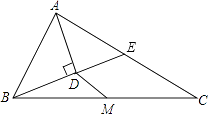
(1)求证:BD=DE;
(2)求DM的长.
【答案】
(1)证明:∵AD平分∠BAC
∴∠BAD=∠DAE
∵AD⊥BD
∴∠ADB=∠ADE=90°
在△ADB与△ADE中

∴△ADB≌△ADE
∴BD=DE
(2)∵△ADB≌△ADE
∴AE=AB=12
∴EC=AC﹣AE=8
∵M是BC的中点,BD=DE
DM= ![]() EC=4
EC=4
【解析】(1)根据条件可证明△ADB≌△ADE,从而可得BD=DE;(2)由(1)可知:EC=AC﹣AB=8,然后根据中位线即可求出DM
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2014年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2016年底三年共累计投资9.5亿元人民币建设廉租房.若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2016年底共建设了多少万平方米的廉租房?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等腰直角三角形,∠ACB=90°,直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
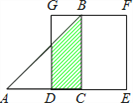
A. 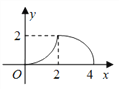 B.
B. 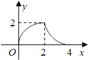 C.
C. 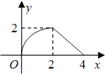 D.
D. 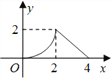
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】至2011年末,南通市户籍人口为764.88万人,将764.88万用科学记数法表示为( )
A.7.6488×104
B.7.6488×105
C.7.6488×106
D.7.6488×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com