
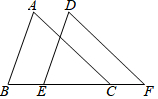
 如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,∠A=∠D.
如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,∠A=∠D. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
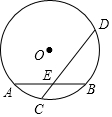 如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )| A. | 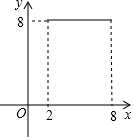 | B. |  | C. | 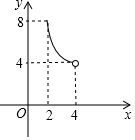 | D. | 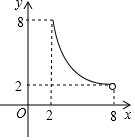 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
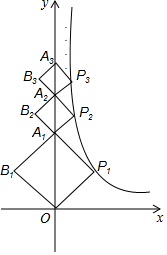 如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、…、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、…、An-1An都在y轴上(n≥1的整数),点P1(x1,y1),点P2(x2,y2),…,Pn(xn,yn)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,并已知B1(-1,1).
如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、…、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、…、An-1An都在y轴上(n≥1的整数),点P1(x1,y1),点P2(x2,y2),…,Pn(xn,yn)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,并已知B1(-1,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
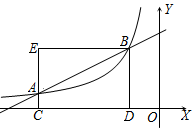 如图,已知A(m,$\frac{1}{2}$)、B(n,2)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的两个交点,且位于第二象限内,过A作AC⊥x轴于C,过B分别作BD⊥x轴于D,BE⊥AC于E,△ABE的面积为$\frac{9}{4}$.
如图,已知A(m,$\frac{1}{2}$)、B(n,2)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的两个交点,且位于第二象限内,过A作AC⊥x轴于C,过B分别作BD⊥x轴于D,BE⊥AC于E,△ABE的面积为$\frac{9}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com