
 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.分析 (1)根据平行四边形的性质得AD∥BC,AD=BC,OB=OD,则利用DM∥BC可判断△MND∽△CNB,所以MD:BC=DN:BN=1:2,设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x-1,于是得到x+1=2(x-1),解得x=3,所以BD=2x=6;
(2)如图,在OD上截取NG=ON,延长OC到H,使HC=OC,则△HOG满足条件.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴DM∥BC,
∴△MND∽△CNB,
∴MD:BC=DN:BN,
∵M为AD中点,
∴MD:BC=1:2,
∴DN:BN=1:2,即BN=2DN,
设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),解得x=3,
∴BD=2x=6;
(2)如图,△HOG为所作.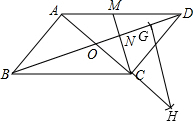
点评 本题考查了作图-位似变换:先确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;再根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了平行四边形的性质.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{{x}^{2}-1}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{a}^{3}b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°
如图所示,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com