
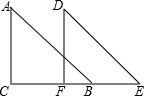
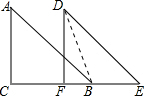
 如图,在△ABC中,∠C=90°,AC=6,AB=10,平移△ABC得到△DEF,且点F在边BC上,DB=3
如图,在△ABC中,∠C=90°,AC=6,AB=10,平移△ABC得到△DEF,且点F在边BC上,DB=3| 5 |
| AB2-AC2 |
| 5 |
| BD2-DF2 |


科目:初中数学 来源: 题型:
| A、某运动员投一次篮,投中的概率为0.8,则该运动员投5次篮,必有4次投中 | ||
| B、抽检1000件衬衣,其中不合格的衬衣有2件,由此估计任抽1件衬衣合格的概率为0.998 | ||
| C、任意抛掷一枚均匀的硬币两次,则第一次正面朝上且第二次背面朝上的概率为0.5 | ||
D、一局国际象棋比赛有胜、负与和局三种结果,你和任一对手下一局棋,出现和局的概率为
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com