
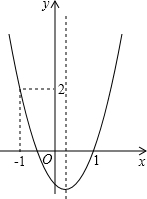
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )| A. | ①⑤ | B. | ①②⑤ | C. | ②⑤ | D. | ①③④ |
分析 先充分挖掘图象所给出的信息,包括对称轴、开口方向、与坐标轴的交点、顶点位置等,然后根据二次函数图象的性质解题.
解答 解:①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为x=-$\frac{b}{2a}$>0,
∴a、b异号,即b<0,
又∵c<0,∴abc>0,
故本选项正确;
②∵对称轴为x=-$\frac{b}{2a}$>0,a>0,-$\frac{b}{2a}$<1,
∴-b<2a,
∴2a+b>0;
故本选项错误;
③当x=1时,y1=a+b+c;
而当x=m时,y=am2+bm+c,
所以a+b+c>am2+bm+c,
故a+b>am2+bm,即a+b>m(am+b),故此选项错误.
④当x=1时,a+b+c=0;
当x=-1时,a-b+c>0;
∴(a+b+c)(a-b+c)=0,即(a+c)2-b2=0,
∴(a+c)2=b2,
故本选项错误;
⑤当x=-1时,a-b+c=2;
当x=1时,a+b+c=0,
∴a+c=1,
∴a=1+(-c)>1,即a>1;
故本选项正确;
综上所述,正确的是①⑤有2个.
故选:A.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换;二次函数y=ax2+bx+c系数符号的确定:
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0;
(2)b由对称轴和a的符号确定:由对称轴公式x=-$\frac{b}{2a}$判断符号;
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0;
(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0,没有交点,b2-4ac<0.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 大量反复抛一均匀硬币,平均100次出现正面朝上50次 | |
| B. | 连续抛一均匀硬币10次都可能正面朝上 | |
| C. | 连续抛一均匀硬币2次必有1次正面朝上 | |
| D. | 通过抛一均匀硬币确定谁先发球的比赛规则是公平的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com