
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯп![]() ЃК
ЃК![]() гы
гы![]() ЃК
ЃК![]() ЯрНЛгкЕуOЁЂCЃЌ
ЯрНЛгкЕуOЁЂCЃЌ![]() гы
гы![]() ЗжБ№НЛxжсгкЕуBЁЂAЃЌЧвBЮЊЯпЖЮAOЕФжаЕуЃЎ
ЗжБ№НЛxжсгкЕуBЁЂAЃЌЧвBЮЊЯпЖЮAOЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєOCЁЭACЃЌЧѓЁїOACЕФУцЛ§ЃЛ
ЃЈ3ЃЉХзЮяЯпC2ЕФЖдГЦжсЮЊlЃЌЖЅЕуЮЊMЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃК
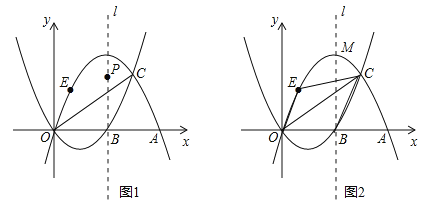
ЂйЕуPЮЊХзЮяЯпC2ЖдГЦжсlЩЯвЛЖЏЕуЃЌЕБЁїPACЕФжмГЄзюаЁЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЂкШчЭМ2ЃЌЕуEдкХзЮяЯпC2ЩЯЕуOгыЕуMжЎМфдЫЖЏЃЌЫФБпаЮOBCEЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіУцЛ§ЕФзюДѓжЕКЭЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂйPЃЈ
ЃЛЃЈ3ЃЉЂйPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЂкEЃЈ
ЃЉЃЛЂкEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩСНХзЮяЯпНтЮіЪНПЩЗжБ№гУaКЭbБэЪОГіAЁЂBСНЕуЕФзјБъЃЌРћгУBЮЊOAЕФжаЕуПЩЕУЕНaКЭbжЎМфЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉгЩХзЮяЯпНтЮіЪНПЩЯШЧѓЕУCЕузјБъЃЌЙ§CзїCDЁЭxжсгкЕуDЃЌПЩжЄЕУЁїOCDЁзЁїCADЃЌгЩЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЕНЙигкaЕФЗНГЬЃЌПЩЧѓЕУOAКЭCDЕФГЄЃЌПЩЧѓЕУЁїOACЕФУцЛ§ЃЛ
ЃЈ3ЃЉЂйСЌНгOCгыlЕФНЛЕуМДЮЊТњзуЬѕМўЕФЕуPЃЌПЩЧѓЕУOCЕФНтЮіЪНЃЌдђПЩЧѓЕУPЕузјБъЃЛ
ЂкЩшГіEЕузјБъЃЌдђПЩБэЪОГіЁїEOBЕФУцЛ§ЃЌЙ§ЕуEзїxжсЕФЦНааЯпНЛжБЯпBCгкЕуNЃЌПЩЯШЧѓЕУBCЕФНтЮіЪНЃЌдђПЩБэЪОГіENЕФГЄЃЌНјвЛВНПЩБэЪОГіЁїEBCЕФУцЛ§ЃЌдђПЩБэЪОГіЫФБпаЮOBCEЕФУцЛ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪПЩЧѓЕУЦфзюДѓжЕЃЌМАEЕуЕФзјБъЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉдкy=x2+axжаЃЌЕБy=0ЪБЃЌx2+ax=0ЃЌx1=0ЃЌx2=ЉaЃЌЁрBЃЈЉaЃЌ0ЃЉЃЌдкy=Љx2+bxжаЃЌЕБy=0ЪБЃЌЉx2+bx=0ЃЌx1=0ЃЌx2=bЃЌЁрAЃЈ0ЃЌbЃЉЃЌЁпBЮЊOAЕФжаЕуЃЌЁрb=Љ2aЃЌЁр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЊСЂСНХзЮяЯпНтЮіЪНПЩЕУЃК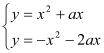 ЃЌЯћШЅyећРэПЩЕУ
ЃЌЯћШЅyећРэПЩЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЁрCЃЈ
ЃЌЁрCЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЙ§CзїCDЁЭxжсгкЕуDЃЌШчЭМ1ЃЌЁрDЃЈ
ЃЉЃЌЙ§CзїCDЁЭxжсгкЕуDЃЌШчЭМ1ЃЌЁрDЃЈ![]() ЃЌ0ЃЉЃЌЁпЁЯOCA=90ЁуЃЌЁрЁїOCDЁзЁїCADЃЌЁр
ЃЌ0ЃЉЃЌЁпЁЯOCA=90ЁуЃЌЁрЁїOCDЁзЁїCADЃЌЁр![]() ЃЌЁрCD2=ADODЃЌМД
ЃЌЁрCD2=ADODЃЌМД![]() ЃЌЁрa1=0ЃЈЩсШЅЃЉЃЌ
ЃЌЁрa1=0ЃЈЩсШЅЃЉЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЌЁрOA=-2a=
ЃЌЁрOA=-2a=![]() ЃЌCD=
ЃЌCD=![]() =1ЃЌЁр
=1ЃЌЁр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйХзЮяЯп![]() ЃЌЁрЦфЖдГЦжс
ЃЌЁрЦфЖдГЦжс![]() ЃЌЕуAЙигкl2ЕФЖдГЦЕуЮЊOЃЈ0ЃЌ0ЃЉЃЌCЃЈ
ЃЌЕуAЙигкl2ЕФЖдГЦЕуЮЊOЃЈ0ЃЌ0ЃЉЃЌCЃЈ![]() ЃЌ1ЃЉЃЌдђPЮЊжБЯпOCгыl2ЕФНЛЕуЃЌЩшOCЕФНтЮіЪНЮЊy=kxЃЌЁр1=
ЃЌ1ЃЉЃЌдђPЮЊжБЯпOCгыl2ЕФНЛЕуЃЌЩшOCЕФНтЮіЪНЮЊy=kxЃЌЁр1=![]() kЃЌЕУk=
kЃЌЕУk=![]() ЃЌЁрOCЕФНтЮіЪНЮЊ
ЃЌЁрOCЕФНтЮіЪНЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЁрPЃЈ
ЃЌЁрPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЩшEЃЈmЃЌ![]() ЃЉЃЈ
ЃЉЃЈ![]() ЃЉЃЌдђ
ЃЉЃЌдђ![]() ЃЌЖјBЃЈ
ЃЌЖјBЃЈ![]() ЃЌ0ЃЉЃЌCЃЈ
ЃЌ0ЃЉЃЌCЃЈ![]() ЃЌ1ЃЉЃЌЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+bЃЌгЩ
ЃЌ1ЃЉЃЌЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+bЃЌгЩ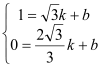 ЃЌНтЕУЃКk=
ЃЌНтЕУЃКk=![]() ЃЌb=-2ЃЌЁржБЯпBCЕФНтЮіЪНЮЊ
ЃЌb=-2ЃЌЁржБЯпBCЕФНтЮіЪНЮЊ![]() ЃЌЙ§ЕуEзїxжсЕФЦНааЯпНЛжБЯпBCгкЕуNЃЌШчЭМ2ЃЌдђ
ЃЌЙ§ЕуEзїxжсЕФЦНааЯпНЛжБЯпBCгкЕуNЃЌШчЭМ2ЃЌдђ![]() ЃЌМДx=
ЃЌМДx=![]()
ЁрEN=![]()
Ёр![]()
ЁрSЫФБпаЮOBCE=SЁїOBE+SЁїEBC![]()
![]() ЃЌЁп
ЃЌЁп![]() ЃЌЁрЕБ
ЃЌЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЁрEЃЈ
ЃЌЁрEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЎ
ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЕуAЃЈ1+mЃЌ1ЉnЃЉгыЕуBЃЈЉ3ЃЌ2ЃЉЙигкyжсЖдГЦЃЌдђm+nЕФжЕЪЧЃЈЁЁЁЁЃЉ
A. Љ5 B. Љ3 C. 3 D. 1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊвЛДЮКЏЪ§y=xЉ1ЕФЭМЯѓОЙ§P1ЃЈx1 ЃЌ y1ЃЉЁЂP2ЃЈx2 ЃЌ y2ЃЉСНЕуЃЌШєx1ЃМx2 ЃЌ дђy1y2ЃЈЬюЁАЃОЁБЃЌЁАЃМЁБЛђЁА=ЁБЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСагяОфе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. 1ЪЧзюаЁЕФздШЛЪ§
B. ЦНЗНЕШгкЫќБОЩэЕФЪ§жЛга1
C. ОјЖджЕзюаЁЕФЪ§ЪЧ0
D. ШЮКЮгаРэЪ§ЖМгаЕЙЪ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЪ§жсЩЯЕуAЃЌBЗжБ№БэЪОЪ§2ЃЌЉ2ЃЌдђAЃЌBСНЕужЎМфЕФОрРыЮЊЃЈЁЁЁЁЃЉ
A. 0B. 4C. Љ2D. Љ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓОЙ§AЃЈ-1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ2ЃЉШ§ЕуЃЎ
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDЪЧИУЖўДЮКЏЪ§ЭМЯѓЩЯЕФвЛЕуЃЌЧвТњзуЁЯDBA=ЁЯCAOЃЈOЪЧзјБъдЕуЃЉЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉЕуPЪЧИУЖўДЮКЏЪ§ЭМЯѓЩЯЮЛгквЛЯѓЯоЩЯЕФвЛЖЏЕуЃЌСЌНгPAЗжБ№НЛBCЃЌyжсгыЕуEЁЂFЃЌШєЁїPEBЁЂЁїCEFЕФУцЛ§ЗжБ№ЮЊS1ЁЂS2ЃЌЧѓS1-S2ЕФзюДѓжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЬт
ЃЈ1ЃЉШє3a=6ЃЌ9b=2ЃЌЧѓ32a+4bЕФжЕЃЛ
ЃЈ2ЃЉвбжЊxy=8ЃЌxЉy=2ЃЌЧѓДњЪ§ЪН ![]() x3yЉx2y2+
x3yЉx2y2+ ![]() xy3ЕФжЕЃЎ
xy3ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇСЫНтБОаЃбЇЩњЖдЧђРрдЫЖЏЕФАЎКУЧщПіЃЌЗжЮЊзуЧђЁЂРКЧђЁЂХХЧђЁЂЦфЫћЫФИіЗНУцЕїВщШєИЩУћбЇЩњЃЌУПШЫжЛбЁЦфжажЎвЛЃЌЭГМЦКѓЛцжЦГЩВЛЭъећЕФЁАелЯпЭГМЦЭМЁБЃЈЩШаЮЭГМЦЭМЃЉЃЌИљОнаХЯЂНтД№ЯТСаЮЪЬтЃК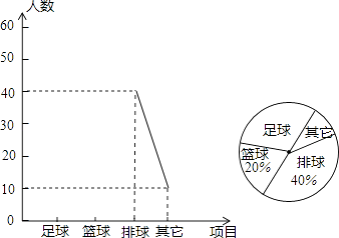
ЃЈ1ЃЉдкетДЮЕїВщжаЃЌвЛЙВЕїВщУћбЇЩњЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЁАзуЧђЁБЫљдкЩШаЮдВаФНЧЖШЃЛ
ЃЈ3ЃЉНЋелЯпЭГМЦЭМВЙГфЭъећЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com