
分析 (1)先计算负整数指数幂、特殊角的三角函数值、零指数幂,然后计算加减法;
(2)由a2+3a-1=0得到a2+3a=1,整体代入所求的代数式.
解答 解:(1)原式=-1-4×$\frac{1}{2}$+1+9=7;
(2)∵a2+3a-1=0,
∴a2+3a=1,
∴(a-$\frac{1}{a}$)÷$\frac{a-1}{(a+1)^{2}-1}$=$\frac{(a+1)(a-1)}{a}$×$\frac{a(a+2)}{a-1}$=(a+1)(a+2)=a2+3a+2=1+2=3.
点评 本题考查了分式的化简求值,实数的运算以及特殊角的三角函数值等知识点,解答(2)题时,注意整体代入数学思想的应用.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
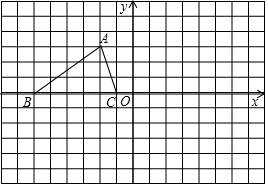 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从与旗杆AB相距27m的点C处,用测角仪CD测得旗杆顶端A的仰角为30°,已知测角仪CD的高为1.5米,则旗杆AB的高约为17.1m(精确到0.1m,参考数据$\sqrt{3}$≈1.73)
如图,从与旗杆AB相距27m的点C处,用测角仪CD测得旗杆顶端A的仰角为30°,已知测角仪CD的高为1.5米,则旗杆AB的高约为17.1m(精确到0.1m,参考数据$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
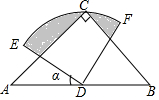 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠ADE=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠ADE=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )| A. | 由小变大 | B. | 由大变小 | ||
| C. | 不变 | D. | 先由小变大,后由大变小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com