
【题目】某课桌生产厂家研究发现,倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长.
(2)如图3,当∠BAC=12°,求AD的长(结果保留根号).
[参考数据:sin24°=0.40,cos24°=0.91,tan24°=0.46,sin12°=0.20]
【答案】
(1)
解:在Rt△ACD中,∵∠DAC=24°,∠ADC=90°,
∴sin24°= ![]() ,
,
∴CD=ACsin24°=30×0.40=12cm;
∴此时支撑臂CD的长为12cm
(2)
解:如图2,过点C作CE⊥AB于点E,
当∠BAC=12°时,
∴sin12°= ![]() =
= ![]() ,
,
∴CE=30×0.20=6cm,
∵CD=12cm,
∴DE= ![]() =
= ![]() =6
=6 ![]() cm,
cm,
∴AE= ![]() =12
=12 ![]() cm,
cm,
如图3有两种情况:
∴AD的长为(12 ![]() +6
+6 ![]() )cm或(12
)cm或(12 ![]() ﹣6
﹣6 ![]() )cm.
)cm.

【解析】(1)在Rt△ACD中利用锐角三角函数关系得出sin24°= ![]() ,代入数值计算即可求出CD的长;(2)过点C作CE⊥AB于点E,在Rt△ACE中利用锐角三角函数关系得出sin12°=
,代入数值计算即可求出CD的长;(2)过点C作CE⊥AB于点E,在Rt△ACE中利用锐角三角函数关系得出sin12°= ![]() ,求出CE的长,再根据勾股定理求出DE,AE的长,进而得出AD的长.
,求出CE的长,再根据勾股定理求出DE,AE的长,进而得出AD的长.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( ) 
A.BO=OH
B.DF=CE
C.DH=CG
D.AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC. 
(1)求证:EC平分∠AEB;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.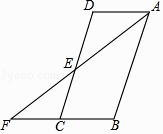
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AB= ![]() ,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( ) 
A.![]()
B.![]()
C.1
D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+4x+m(m为常数)经过点(0,4)
(1)求m的值;
(2)将该抛物线先向右、再向下平移得到另一条抛物线.已知这条平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为l1)关于y轴对称;它所对应的函数的最小值为﹣8.
①试求平移后的抛物线所对应的函数关系式;
②试问在平移后的抛物线上是否存在着点P,使得以3为半径的⊙P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被⊙P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com