已知△ABC,AB=AC=5,BC=8,若⊙O只与△ABC的两边相切,且切点均在边上,则⊙O的半径r的取值范围是 .
【答案】
分析:过A点作AD⊥BC于D,根据等腰三角形的性质得到BD=DC=4,AD平分∠BAC,利用勾股定理得AD=3;若⊙O只与△ABC的AB、AC两边相切,则圆心O在AD上,当切点分别为点B和点C时,⊙O的半径r最大,连OB、OC,易证Rt△ABD∽Rt△AOB,利用相似比可求出OD=
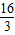
,在Rt△OBD中利用勾股定理可计算出OB=
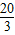
,而当圆心在O′时,与三边都相切,设与AB的切点为E,连O′E,易证Rt△AEO′∽Rt△ADB,利用相似比可求出OD=

;若⊙O只与△ABC的BA、BC两边相切,当A为切点时,⊙O的半径r最大,最大半径小于AD=3,由此得到⊙O的半径r的取值范围是0<r≤
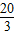
,且r≠

.
解答: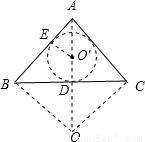
解:过A点作AD⊥BC于D,如图,
∵AB=AC=5,BC=8,
∴BD=DC=4,AD平分∠BAC,
∴AD=

=3;
若⊙O只与△ABC的AB、AC两边相切,则圆心O在AD上
当切点分别为点B和点C时,⊙O的半径r最大,
连OB、OC,如图,
∴OB⊥AB,
∴Rt△ABD∽Rt△AOB,
∴AB:AO=AD:AB,即5:(OD+3)=3:5,
∴OD=
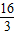
,
在Rt△OBD中,
OB=
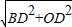
=
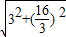
=
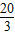
,
而当圆心在O′时,与三边都相切,设与AB的切点为E,连O′E,如图,
则O′E⊥AB,O′E=O′D,
∴Rt△AEO′∽Rt△ADB,
∴O′E:BD=AO′:AB,即O′E:4=(3-O′E):5,
∴O′E=

,
∴⊙O的半径r的取值范围是0<r≤
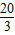
,且r≠

;
若⊙O只与△ABC的BA、BC两边相切,
当A为切点时,⊙O的半径r最大,最大半径小于AD=3,
所以⊙O的半径r的取值范围是0<r≤
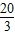
,且r≠

.
故答案为0<r≤
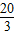
,且r≠

.
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了等腰三角形的性质、勾股定理以及三角形相似的判定与性质.

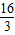 ,在Rt△OBD中利用勾股定理可计算出OB=
,在Rt△OBD中利用勾股定理可计算出OB=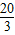 ,而当圆心在O′时,与三边都相切,设与AB的切点为E,连O′E,易证Rt△AEO′∽Rt△ADB,利用相似比可求出OD=
,而当圆心在O′时,与三边都相切,设与AB的切点为E,连O′E,易证Rt△AEO′∽Rt△ADB,利用相似比可求出OD= ;若⊙O只与△ABC的BA、BC两边相切,当A为切点时,⊙O的半径r最大,最大半径小于AD=3,由此得到⊙O的半径r的取值范围是0<r≤
;若⊙O只与△ABC的BA、BC两边相切,当A为切点时,⊙O的半径r最大,最大半径小于AD=3,由此得到⊙O的半径r的取值范围是0<r≤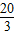 ,且r≠
,且r≠ .
. 解:过A点作AD⊥BC于D,如图,
解:过A点作AD⊥BC于D,如图, =3;
=3;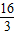 ,
,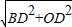 =
=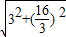 =
=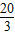 ,
, ,
,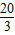 ,且r≠
,且r≠ ;
;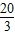 ,且r≠
,且r≠ .
.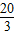 ,且r≠
,且r≠ .
.

