练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数y=x2﹣4x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x2﹣4x+m=0的两个实数根是（ ）
    A.x1=1，x2=﹣1
    B.x1=﹣1，x2=2
    C.x1=﹣1，x2=0
    D.x1=1，x2=3

    【答案】D
    【解析】解：∵二次函数y=x2﹣4x+m（m为常数）的图象与x轴的一个交点为（1，0）， ∴关于x的一元二次方程x2﹣4x+m=0的一个根是x=1．
    ∴设关于x的一元二次方程x2﹣4x+m=0的另一根是t．
    ∴1+t=4，
    解得 t=3．
    即方程的另一根为3．
    故选：D．
    根据抛物线与x轴交点的性质和根与系数的关系进行解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】化简|π﹣4|+|3﹣π|= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中，假命题是（ ）

    A. 三角形的一个外角大于任何一个不相邻的内角

    B. 三角形按边可分为不等边三角形、等腰三角形、等边三角形、

    C. 三角形中最少有2个锐角

    D. 三角形的三条中线交于一点，这个交点就是三角形的重心

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一元二次方程3x2﹣5=4x化为一般形式后，二次项系数和一次项系数分别是（ ）
    A.﹣3，4
    B.3，﹣4
    C.﹣3，﹣4
    D.3，4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下面的解题过程的横线上填空，并在括号内注明理由． 如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．
    解：∵∠A=∠F（已知）
    ∴AC∥DF（）
    ∴∠D=∠（）
    又∵∠C=∠D（已知）
    ∴∠1=∠C（等量代换）
    ∴BD∥CE（）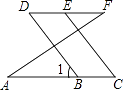

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于任意两个有理数a、b，规定ab=3a﹣b，若（2x+3）（3x﹣1）=4，则x的值为（　　）

    A. 1 B. ﹣1 C. 2 D. ﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是一名学生所做的4道练习题：①﹣22=4②a3+a3=a6③4m﹣4= ④（xy2）3=x3y6 ， 他做对的个数（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在边长为4的菱形ABCD中，AC为其对角线，∠ABC=60°点M、N是分别是边BC、边CD上的动点，且MB=NC．连接AM、AN、MN．MN交AC于点P．

    （1）△AMN是什么特殊的三角形？说明理由．并求其面积最小值；

    （2）求点P到直线CD距离的最大值；

    （3）如图2，已知MB=NC=1，点E、F分别是边AM、边AN上的动点，连接EF、PF，EF+PF是否存在最小值？若存在，求出最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知|x|=2，y=x﹣3，则y的值为（　　）

    A. 5 或﹣1 B. ﹣1 或﹣5 C. 1 D. ﹣1

    查看答案和解析>>

    同步练习册答案