
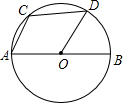
 如图,已知AB是⊙O的直径,弦AC与半径OD平行.
如图,已知AB是⊙O的直径,弦AC与半径OD平行.分析 (1)欲证弧BD=弧CD,只需证明它们所对的圆心角相等,即∠BOD=∠COD.
解答 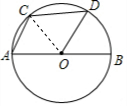 (1)证明:如图,连接OC.
(1)证明:如图,连接OC.
∵OA=OC,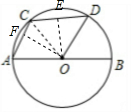
∴∠OAC=∠ACO.
∵AC∥OD,
∴∠OAC=∠BOD.
∴∠DOC=∠ACO.
∴∠BOD=∠COD.
∴弧BD=弧CD;
(2)∵tan∠CDO=$\sqrt{2}$,∴tan∠DOE=$\frac{\sqrt{2}}{2}$,∴tan∠COD=tan∠FOA=tan2∠DOE=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×\frac{\sqrt{2}}{2}}{1-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{2}}{\frac{1}{2}}$=2$\sqrt{2}$,∴cosα=$\frac{1}{9}$
∴$\frac{\frac{1}{2}AC}{OD}$=cosα=$\frac{1}{9}$,∴$\frac{AC}{OD}$=$\frac{2}{9}$
tan(2α)=2tanα/(1-tan22α)
点评 MM


科目:初中数学 来源: 题型:解答题
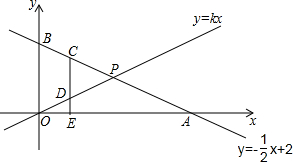 一次函数y=-$\frac{1}{2}$x+2的图象在平面直角坐标系中交x轴、y轴分别于A、B两点,交直线y=kx于P.
一次函数y=-$\frac{1}{2}$x+2的图象在平面直角坐标系中交x轴、y轴分别于A、B两点,交直线y=kx于P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com