已知A(4,0)、B(0,4)
(1)求直线AB的解析式;
(2)点P从A点出发沿x轴向O点运动,点Q从O点出发沿y轴向B点运动,两点同时出发且运动速度相同.设AP=t﹙0<t<4﹚,求直线PQ的解析式;
(3)M是线段AB的中点,在(2)的条件下,试判断△MPQ的形状,并说明理由.
解:(1)设直线AB的解析式是:y=kx+b,
把A(4,0),B(0,4)代入得:

,
解得:k=-1,b=4,
∴y=-x+4,
答:直线AB的解析式是y=-x+4.
(2)根据题意得:∵AP=t,
∴OQ=AP=t,OP=4-t,
∴Q(0,t),P(4-t,0),
设直线PQ的解析式是y=ax+c,
把P、Q的坐标代入得:

解得:a=

,c=t,
∴
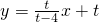
,

答:直线PQ的解析式是
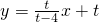
.
(3)△MPQ的形状是等腰直角三角形,
理由是:连OM,
∵OA=OB,M为AB的中点,
∴OM⊥AB,OM=AM=BM,OM平分∠AOB,
∴∠BAO=∠BOM=45°,
∵AP=OQ,
∴△MOQ≌△MAP,
∴MQ=MP,∠QMO=∠AMP,
∴∠QMO+∠OMP=∠OMP+∠PMA=90°,
即∠QMP=90°,
∴△MPQ为等腰直角三角形.
分析:(1)设直线AB的解析式是:y=kx+b,把A(4,0),B(0,4)代入得到方程组,求出方程组的解即可;
(2)求出Q、P的坐标,设直线PQ的解析式是y=ax+c,把P、Q的坐标代入得到方程组,求出方程组的解即可;
(3)根据等腰三角形的性质求出OM⊥AB,OM=AM=BM,OM平分∠AOB,证△MOQ≌△MAP,推出MQ=MP,∠QMO=∠AMP即可.
点评:本题主要考查对解二元一次方程组,用待定系数法求一次函数的解析式,等腰直角三角形的判定,等腰三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

 ,
,
 ,c=t,
,c=t,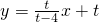 ,
,
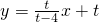 .
.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.