
【题目】(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是_____________________;
(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
(3)结论应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.

【答案】(1)EF=BE+DF;(2)EF=BE+DF仍然成立;(3)210海里.
【解析】
(1)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(2)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(3)连接EF,延长AE、BF相交于点C,然后与(2)同理可证.
解:(1)EF=BE+DF
(2)EF=BE+DF仍然成立
证明如下:延长FD到G,使DG=BE,
连接AG,如图2
∵∠B+∠ADC=180°
∠ADC+∠ADG=180°
∴∠B=∠ADG
在△ABE和△ADG中

∴△ABE≌△ADG(SAS)
∴AE=AG,∠BAE=∠DAG
∵∠EAF=∠BAD
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=![]() ∠BAD
∠BAD
∴∠EAF=∠GAF
在△AEF和△GAF中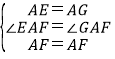
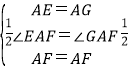
∴△AEF≌△AGF(SAS)
∴EF=FG
∵FG=DG+DF
∴EF=BE+DF
(3)如图,连接EF,延长AE、BF相交于点C
由题意得:∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°
∴∠EOF=∠AOB
又∵OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°
∴符合(2)的条件
∴结论EF=AE+BF成立
∴ EF=1.5×(60+80)=210海里
答:此时两舰艇之间的距离是210海里.


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是∠ABC平分线,DE![]() AB于E,AB=36cm,BC=24cm,S△ABC =144cm2,则DE的长是( )
AB于E,AB=36cm,BC=24cm,S△ABC =144cm2,则DE的长是( )

A. 4.8cm B. 4.5cm C. 4 cm D. 2.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
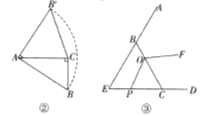
【题目】(1)观察推理:如图①,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l的同侧,,垂足分别为.求证:△AEC≌△CDB.
(2)类比探究:如图②,在Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB,,连接CB,,求△ACB,的面积.
(3)拓展提升:如图③,在△EBC中,∠E=∠ECB=60°,EC=BC=3,点O在BC上,且OC=2,动点P从点E沿射线EC以每秒1个单位长度的速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点 F恰好落在射线EB上,求点P运动的时间t.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN;

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( ) 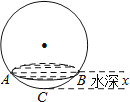
A.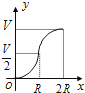
B.
C.
D.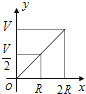
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列数组作为三角形的三条边长,其中能构成直角三角形的是( )
A. 1, ![]() ,3 B.
,3 B. ![]() ,
, ![]() ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D. ![]() ,
, ![]() ,
, ![]()
【答案】C
【解析】A、12+(![]() )2≠32,不能构成直角三角形,故选项错误;
)2≠32,不能构成直角三角形,故选项错误;
B、(![]() 2+(
2+(![]() )2≠52,不能构成直角三角形,故选项错误;
)2≠52,不能构成直角三角形,故选项错误;
C、1.52+22=2.52,能构成直角三角形,故选项正确;
D、(![]() ))2+(
))2+(![]() )2≠(
)2≠(![]() )2,不能构成直角三角形,故选项错误.
)2,不能构成直角三角形,故选项错误.
故选:C.
【题型】单选题
【结束】
3
【题目】在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A)![]() (B)
(B)![]() (C)9 (D)6
(C)9 (D)6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com