Question

19．从点P向⊙O引两条切线PA，PB，切点为A，B，AC为弦，BC为⊙O直径，若∠P=60°，PB=2cm，求：
①半径；
②求AB；
③AC的长．

Answer 1

分析 连接AB、OP，AB与OP相交于点D，①先证明Rt△PAO≌Rt△PBO，从而得到∠BPO=30°，依据特殊锐角三角函数值可求得OB=$\frac{2\sqrt{3}}{3}$；②由切线长定理可知PA=PB，然后证明△PAB为等边三角形，于是得到AB=PB=2；③证明△AOC为等边三角形即可．

解答 解：如图所示：连接AB、OP，AB与OP相交于点D．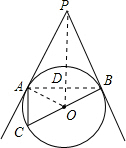

①∵PA、PB是圆O的切线，
∴∠PAO=∠PBO=90°．
在Rt△PAO和Rt△PBO中，
$\left\{\begin{array}{l}{OA=OB}\\{PO=PO}\end{array}\right.$，
∴Rt△PAO≌Rt△PBO．
∴∠BPO=APO．
∴∠BPO=30°．
∴$\frac{OB}{PB}=\frac{\sqrt{3}}{3}$，即$\frac{OB}{2}=\frac{\sqrt{3}}{3}$．
∴OB=$\frac{2\sqrt{3}}{3}$．
②∵PA、PB是圆O的切线，
∴PA=PB．
又∵∠APB=60°，
∴△PAB为等边三角形．
∴AB=PB=2．
③∵∠PAO=∠PBO=90°，
∴∠P+∠AOB=180°．
∴∠AOB=120°．
∴∠AOC=60°．
又∵OA=OC，
∴△AOC为等边三角形．
∴AC=$\frac{2\sqrt{3}}{3}$．

点评 本题主要考查的是切线长定理、等边三角形的性质和判定、特殊锐角三角函数值的应用、全等三角形的判定，掌握本题的辅助线的作法是解题的关键．