

���� ��1���ɵ���ֱ�������ε����ʵó���COB=90�㣬��B=45�㣬��OCB=45�㣬OC=$\frac{1}{2}$AB=OA=OB��ͬ����OD=OF����SAS֤����DOC�ա�FOB�����ɵó����ۣ�
��2������OD��֤����DOC=��FOB����SAS֤����DOC�ա�FOB�����ɵó����ۣ�
��3��֤����CDG=��BDH����ASA֤����CDG�ա�BDH���ó���Ӧ�����DG=DH�����ɵó����ۣ�
��� ��1��֤������OC�ǵ���Rt��ABC�ĵױ�AB�ϵĸߣ�
���COB=90�㣬��B=45�㣬��OCB=45�㣬OC=$\frac{1}{2}$AB=OA=OB��
ͬ����OD=OF��
�ڡ�DOC�͡�FOB�У�$\left\{\begin{array}{l}{OC=OF}&{\;}\\{��COD=��BOF=90��}&{\;}\\{OC=OB}&{\;}\end{array}\right.$��
���DOC�ա�FOB��SAS����
��BF=CD��
��2���⣺��1���еĽ����ڳ�������������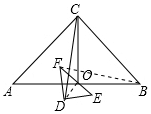
����OD��BF����ͼ��ʾ��
�ߡ�DOC=��DOF+��FOC=90��+��FOC����FOB=��COB+��FOC=90��+��FOC��
���DOC=��FOB��
�ڡ�DOC�͡�FOB�У�$\left\{\begin{array}{l}{OC=OF}&{\;}\\{��COD=��BOF=90��}&{\;}\\{OC=OB}&{\;}\end{array}\right.$��
���DOC�ա�FOB��SAS����
��BF=CD��
��3��FG=EH���������£�
�ߡ�BDC=��EDF=90�㣬
���CDG=��BDH��
�ڡ�CDG�͡�BDH�У�$\left\{\begin{array}{l}{��GCD=��B=45��}&{\;}\\{CD=BD}&{\;}\\{��CDG=��BDH}&{\;}\end{array}\right.$��
���CDG�ա�BDH��ASA����
��DG=DH��
�֡�DF=DE��
��FG=EH��
���� �������������ۺ���Ŀ�������˵���ֱ�������ε����ʡ�ȫ�������ε��ж������ʣ��������յ���ֱ�������ε����ʣ�֤��������ȫ���ǽ������Ĺؼ���


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 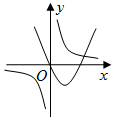 | B�� |  | C�� | 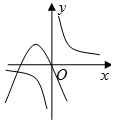 | D�� | 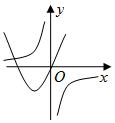 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | 0 | C�� | $\root{3}{27}$ | D�� | $\sqrt{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 20 | C�� | 26 | D�� | -26 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
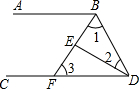 ��ͼ����ABD�͡�BDC��ƽ�����ཻ�ڵ�E��BE��CD�ڵ�F����1+��2=90�㣬�Բ��룺ֱ��AB��CD��λ������ʲô��ϵ����2�͡�3����������ʲô��ϵ����֤����IJ��룮
��ͼ����ABD�͡�BDC��ƽ�����ཻ�ڵ�E��BE��CD�ڵ�F����1+��2=90�㣬�Բ��룺ֱ��AB��CD��λ������ʲô��ϵ����2�͡�3����������ʲô��ϵ����֤����IJ��룮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com