
分析 (1)根据正比例函数定义分别设出y、z的函数解析式,再表示出z与x间的关系即可判断;
(2)根据正比例函数的定义由常数项为0可得.
解答 解:(1)根据题意,设y=m(x+2),z=n(y-1)
∴z=n[m(x+2)-1]=n(mx+2m-1)=mnx+n(2m-1)
∴z是x的一次函数;
(2)根据题意,n(2m-1)=0
∵m≠0,n≠0,
∴m=$\frac{1}{2}$,
故当m=$\frac{1}{2}$时,z是x的正比例函数.
点评 此题主要考查了一次函数、正比例函数的定义,在一次函数解析式y=kx+b(k≠0)中,特别注意不要忽略k≠0这个条件,当b=0时,该函数为正比例函数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
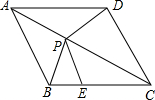 如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.
如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
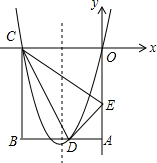 如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系.
如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )| A. | 1200$+270\sqrt{2}$ | B. | 800$+270\sqrt{2}$ | C. | 540$+600\sqrt{2}$ | D. | 800$+600\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com