
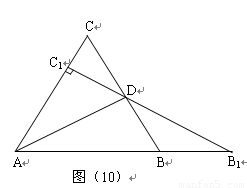
如图(10)所示:等边△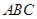 中,线段
中,线段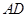 为其内角平分线,过
为其内角平分线,过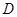 点的直线
点的直线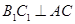 于
于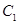 交
交 的延长线于
的延长线于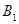 .
.
1.请你探究: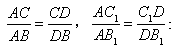 ,是否成立?
,是否成立?
2.请你继续探究:若△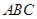 为任意三角形,线段
为任意三角形,线段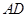 为其内角平分线,请问
为其内角平分线,请问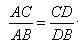 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
3.
1.结论成立
∵△ABC为等边三角形,AD为角平分线,
∴AD垂直平分BC,∠CAD=∠BAD=30°,AB=AC,
∴DB=CD,
∴AC AB =CD DB ;
∵∠C1AB1=60°,
∴∠B1=30°,
∴AB1=2AC1,
又∵∠DAB1=30°,
∴DA=DB1,
而DA=2DC1,
∴DB1=2DC1,
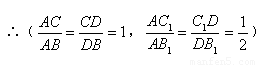
2.结论成立,理由如下:
如图,过点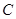 作
作 ∥
∥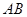 交
交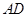 的延长线于点
的延长线于点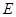 ,则
,则

3.由勾股定理可求

【解析】本题考查了相似三角形的判定与性质:平行于三角形一边的直线被其它两边所截,所截得的三角形与原三角形相似;相似三角形对应边的比相等.也考查了等边三角形的性质、含30°的直角三角形三边的关系以及角平分线的性质


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,点P1,P2,P3,…,P10在反比例函数y=
如图所示,点P1,P2,P3,…,P10在反比例函数y=| 6 |
| x |
A、Q10(
| ||
B、Q10(
| ||
C、Q10(
| ||
| D、Q10(19,0) |
查看答案和解析>>
科目:初中数学 来源:2012届初中毕业生学业考试(湖北黄石卷)数学(带解析) 题型:解答题
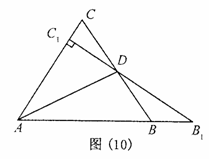
如图(10)所示:等边△ 中,线段
中,线段 为其内角平分线,过
为其内角平分线,过 点的直线
点的直线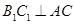 于
于 交
交 的延长线于
的延长线于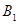 .
.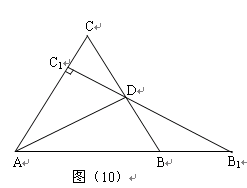
【小题1】请你探究: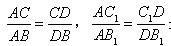 ,是否成立?
,是否成立?
【小题2】请你继续探究:若△ 为任意三角形,线段
为任意三角形,线段 为其内角平分线,请问
为其内角平分线,请问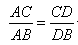 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
【小题3】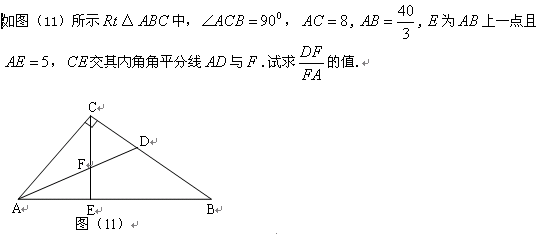
查看答案和解析>>
科目:初中数学 来源: 题型:
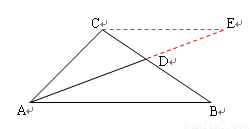
如图(10)所示:等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于C1交AB的延长线于B1.
⑴请你探究:![]() ,
,![]() 是否都成立?
是否都成立?
⑵请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
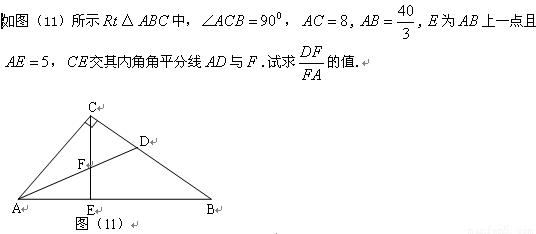
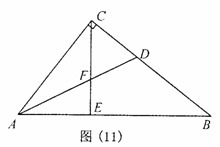
⑶如图(11)所示Rt△ABC中,∠ACB=90︒,AC=8,AB=![]() ,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求
,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com