练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】“一方有难，八方支援”，雅安芦山420地震后，某单位为一中学捐赠了一批新桌椅，学校组织初一年级200名学生搬桌椅．规定一人一次搬两把椅子，两人一次搬一张桌子，每人限搬一次，最多可搬桌椅（一桌一椅为一套）的套数为（ ）
    A.60
    B.70
    C.80
    D.90

    【答案】C
    【解析】解：设可搬桌椅x套，即桌子x张、椅子x把，则搬桌子需2x人，搬椅子需 人，
    根据题意，得：2x+ ≤200，
    解得：x≤80，
    ∴最多可搬桌椅80套，
    故选：C．
    设可搬桌椅x套，即桌子x张、椅子x把，则搬桌子需2x人，搬椅子需 人，根据总人数列不等式求解可得．本题主要考查一元一次不等式的应用能力，设出桌椅的套数，表示出搬桌子、椅子的人数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD内接于⊙O， ： ： =2：3：5，∠BAD=120°，则∠ABC的度数为（ ）
    A.100°
    B.105°
    C.120°
    D.125°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在每个小正方形的边长为1的网格中，A，E为格点，B，F为小正方形边的中点，C为AE，BF的延长线的交点．

    （1）AE的长等于；
    （2）若点P在线段AC上，点Q在线段BC上，且满足AP=PQ=QB，请在如图所示的网格中，用无刻度的直尺，画出线段PQ，并简要说明点P，Q的位置是如何找到的（不要求证明） ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A，O旋转后的对应点为A′，O′，记旋转角为α．

    （1）如图①，若α=90°，求AA′的长；
    （2）如图②，若α=120°，求点O′的坐标；
    （3）在（Ⅱ）的条件下，边OA上 的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，求点P′的坐标（直接写出结果即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲乙两人进行射击训练，两人分别射击12次，如图分别统计了两人的射击成绩，已知甲射击成绩的方差S甲2= ，平均成绩 =8.5．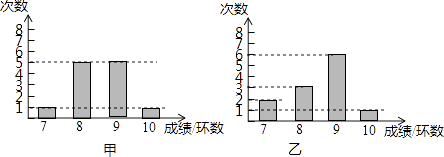

    （1）根据图上信息，估计乙射击成绩不少于9环的概率是多少？
    （2）求乙射击的平均成绩的方差，并据此比较甲乙的射击“水平”．
    S2= [（x1﹣ ）2+（x2﹣ ）2…（xn﹣ ）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲乙二人在环形跑道上同时同地出发，同向运动．若甲的速度是乙的速度的2倍，则甲运动2周，甲、乙第一次相遇；若甲的速度是乙的速度3倍，则甲运动 周，甲、乙第一次相遇；若甲的速度是乙的速度4倍，则甲运动 周，甲、乙第一次相遇，…，以此探究正常走时的时钟，时针和分针从0点（12点）同时出发，分针旋转周，时针和分针第一次相遇．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图:

    (1)试验观察:

    如果经过两点画直线,那么:

    第①组最多可以画____条直线;

    第②组最多可以画____条直线;

    第③组最多可以画____条直线.

    (2)探索归纳:

    如果平面上有n(n≥3)个点,且任意3个点均不在1条直线上,那么经过两点最多可以画____条直线.(用含n的式子表示)

    (3)解决问题:

    某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握____次手.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为4的正方形ABCD内接于点O，点E是 上的一动点（不与A、B重合），点F是 上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论： ① = ；
    ②△OGH是等腰三角形；
    ③四边形OGBH的面积随着点E位置的变化而变化；
    ④△GBH周长的最小值为4+ ．
    其中正确的是（把你认为正确结论的序号都填上）．

    查看答案和解析>>

    同步练习册答案