
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)与 x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,-3).
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)与 x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,-3).分析 (1)根据图象与y轴的交点,可得m的值,可得函数解析式;
(2)根据线段垂直平分线上的点到线段两端点的距离相等,可得M在对称轴上,根据两点之间线段最短,可得M点在线段AB上,根据自变量与函数值的对应关系,可得答案;
(3)根据一次函数图象与区域抛物线的交点,可得不等式组,根据解不等式组,可得答案.
解答 解:(1)由题意可得,m-4=-3.∴m=1.
∴抛物线的解析式为:y=x2-2x-3.
(2)如图,点A关于抛物线的对称轴对称的点是B,
连接BC交对称轴于点P,
则点P就是使得PA+PC的值最小的点.
由y=x2-2x-3,得对称轴是x=1,
由B(3,0),C(0,-3),得
直线BC的解析式为y=x-3,
当x=1时,y=1-3=-2,
∴点P的坐标为(1,-2).
(3)当x=0时,直线y=5x+b≤-3,
解得b≤-3;
直线y=5x+b与抛物线相切时,得
x2-7x-(3+b)=0,
49+4(3+b)≥0,
解得b≥-$\frac{61}{4}$,
符合题意的b的取值范围是-$\frac{61}{4}$≤b≤-3.
点评 本题考察了二次函数综合题,利用线段垂直平分线上的点到线段两端点的距离相等得出M在对称轴上是解题关键.


科目:初中数学 来源: 题型:选择题
 如图,甲从A点出发向北偏东70°走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )
如图,甲从A点出发向北偏东70°走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )| A. | 125° | B. | 160° | C. | 85° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1,1 | B. | -1,1,2 | C. | -1,0,1 | D. | 0,1,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面上有四个点A,B,C,D.
如图,平面上有四个点A,B,C,D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
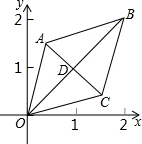 如图,已知菱形OABC的顶点O(0,0),B(2,2),菱形的对角线的交点D的坐标为(1,1);菱形OABC绕点O逆时针旋转,每秒旋转45°,从如图所示位置起,经过60秒时,菱形的对角线的交点D的坐标为(-1,-1).
如图,已知菱形OABC的顶点O(0,0),B(2,2),菱形的对角线的交点D的坐标为(1,1);菱形OABC绕点O逆时针旋转,每秒旋转45°,从如图所示位置起,经过60秒时,菱形的对角线的交点D的坐标为(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com