
������֣�
��ͼ1����O��Rt��ABC�����Բ����ABC=90�㣬��BD=BA��BE��DC��DC���ӳ����ڵ�E����֤��BE�ǡ�O�����ߣ�
���������
����OB��Ҫ֤��BE�ǡ�O�����ߣ�ֻҪ֤��OB ____ BE��������֪��E=90�㣬��ֻ��֤��OB ___ DE��
�ⷨ̽����
��1��С��������������������̽�����벹ȫ����֤��˼·��
��ͼ2������AD���ɡ�ECB��Բ�ڽ��ı���ABCD��һ����ǣ���֤��ECB=��BAD����ΪOB=OC������ __ ����ΪBD=BA������ ______ ������ͬ�����Ե�Բ�ܽ���Ⱥ͵����������õ� ____ ������DE��OB���Ӷ�֤����BE�ǡ�O�����ߣ�
��2����ͼ3������AD����ֱ��BF��AD�ڵ�H��С������BF��AD����˵�����ɣ�
��3������С���ķ��֣���֤��BE�ǡ�O�����ߣ���Ҫ��������ֲ�ͬ��֤����������


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ������Ͽ������꼶��������ѧ�Ծ��������棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У���֪��A��3��4������OA������ԭ��O��ʱ����ת90����OA�䣬���A��������� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭�����������о��꼶��9�¶ο���ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪��O��ֱ��Ϊ8���ҵ�P�ڡ�O�ڣ����߶�PO�ij��ȣ� ��
A����8 B������8 C������4 D����4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭����ʦ������о��꼶��10�¿���ѧ�Ծ��������棩 ���ͣ������
��������ε�һ���ڽǵ���150�㣬�����������εı����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭����ʦ������о��꼶��10�¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
2010��3�·ݣ�ij������һ�ܿ�������������ij����Ⱦָ���������ǣ�31��35��31��34��30��32��31���������ݵ���λ���������ֱ��ǣ� ��
A��32��31 B��31��32 C��31��31 D��32��35
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭���Ͼ���¥�����꼶��������ѧ�Ծ��������棩 ���ͣ������
����֪��������̵Ľⷨ��Ȼ������ͬ���������ǵĻ���˼�붼�ǡ�ת����������δ֪ת��Ϊ��֪���á�ת��������ѧ˼�룬���ǻ����Խ�һЩ�·��̣�
��ʶ�·��̣�
�� =x�����������º���δ֪���ķ��̽����������̣�����ͨ����������ƽ������ת��Ϊ2x+3=x2�����x1=3��x2=��1������������ƽ�������ܲ���������������Ҫ���飬�����飬x2=��1��ԭ���̵���������ȥ������ԭ���̵Ľ���x=3��
=x�����������º���δ֪���ķ��̽����������̣�����ͨ����������ƽ������ת��Ϊ2x+3=x2�����x1=3��x2=��1������������ƽ�������ܲ���������������Ҫ���飬�����飬x2=��1��ԭ���̵���������ȥ������ԭ���̵Ľ���x=3��
�������Ͼ��飬�����з��̣�
��1��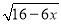 =x��
=x��
��2��x+2 =6��
=6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭���Ͼ���¥�����꼶��������ѧ�Ծ��������棩 ���ͣ������
��һ��������ֽ�尴��ͼ��ʾ�ķ�ʽ����һ��������������ϣ�ʹ��C���ڰ�Բ�ϣ�����A��B���Ķ����ֱ�Ϊ65�㡢20�㣬���ACB�Ĵ�СΪ �㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�켪�ֳ�����У���о��꼶�����У������⣩��ѧ�Ծ��������棩 ���ͣ������
��ͼ����ƽ���ı���ABCD�У���E�ڱ�BC�ϣ�����E��BD��ƽ���߽�DC�ڵ�G����AD���ӳ����ڵ�F��
��1����֤��DF=BE��
��2���� ��BE=2����BC�ij���
��BE=2����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�����������п�ģ����ѧ�Ծ����壩�������棩 ���ͣ�ѡ����
��ͼ����A��B��C��һ��ֱ���ϣ���ABD����BCE��Ϊ�ȱ������Σ�����AE��CD��AE�ֱ�CD��BD�ڵ�M��P��CD��BE�ڵ�Q������PQ��BM��������ۣ�
�١�ABE�ա�DBC���ڡ�DMA=60�㣻�ۡ�BPQΪ�ȱ������Σ���MBƽ�֡�AMC��
���н�����ȷ���У� ��

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com