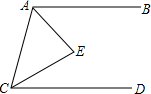
解:(1)∠A+∠P+∠C=360°.
理由:过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠APC=∠A+∠1+∠2+∠C=360°.
(2)∠P=∠A+∠C.
理由:过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠A,∠2=∠C,
∴∠APC=∠1+∠2=∠A+∠C.
(3)∠C=∠A+∠P.
理由:∵AB∥CD,
∴∠1=∠C,
∵∠1=∠A+∠P,
∴∠C=∠A+∠P;
(4)∠A=∠C+∠P.
理由:∵AB∥CD,
∴∠1=∠A,
∵∠1=∠C+∠P,
∴∠A=∠C+∠P.
分析:(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)由AB∥CD,根据两直线平行,同位角相等,即可求得∠1=∠C,又由三角形外角的性质,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角相等,即可求得∠1=∠A,又由三角形外角的性质,即可求得答案.
点评:此题考查了平行线的性质与三角形外角的性质.此题难度不大,解题的关键是注意掌握两直线平行,同位角相等;两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用,注意辅助线的作法.


 解:(1)∠A+∠P+∠C=360°.
解:(1)∠A+∠P+∠C=360°.

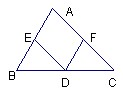 39、填写推理理由
39、填写推理理由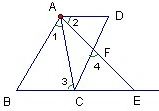 解:∵AB∥CD(已知)
解:∵AB∥CD(已知)