
 阅读下列材料:
阅读下列材料:分析 (1)根据三角函数进行解答即可;
(2)利用直角三角形中的三角函数解答即可.
解答 解:(1)sinα=$\frac{1}{3}$,cosα=$\frac{2\sqrt{2}}{3}$,可得:sin2α=$\frac{{4\sqrt{2}}}{9}$;
故答案为:$\frac{1}{3}$;$\frac{4\sqrt{2}}{9}$
(2)∵AC=cosα,BC=sinα,
∴CD=$\frac{AC×BC}{AB}$=sinα•cosα.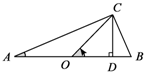
∵∠DCB=∠A,
∴在Rt△BCD中,BD=sin2α.
∴OD=$\frac{1}{2}$-sin2α.
∴tan2α=$\frac{CD}{OD}$=$\frac{sinα•cosα}{\frac{1}{2}-si{n}^{2}α}=\frac{2sinα•cosα}{1-2si{n}^{2}α}$.
点评 本题通过题目提供信息考查了解直角三角形,读懂题目信息并根据信息表示出三角形的三角函数是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{2(a-2)}{a+2}$ | D. | $\frac{2}{(a+2)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$
在平面直角坐标系 xOy中,对于点P(x,y),以及两个无公共点的图形W1和W2,若在图形W1和W2上分别存在点M (x1,y1 )和N (x2,y2 ),使得P是线段MN的中点,则称点M 和N被点P“关联”,并称点P为图形W1和W2的一个“中位点”,此时P,M,N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )| A. | 4 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com