练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图，下列条件中，能判定DE∥AC的是（　　）
    A．∠BED=∠EFCB．∠1=∠2C．∠BEF+∠B=180°D．∠3=∠4

    分析 可以从直线DE、AC的截线所组成的“三线八角”图形入手进行判断．

    解答 解：A、∠BED=∠EFC不是两直线被第三条直线所截得到的，因而不能判定两直线平行，故选项错误；
    B、∠1=∠2是EF和BC被EC所截得到的同位角和内错角，因而可以判定EF∥BC，但不能判定DE∥AC，故选项错误；
    C、∠BEF+∠B=180°是EF和BC被AB所截得到的同旁内角，因而可以判定EF∥BC，但不能判定DE∥AC，故选项错误；
    D、∠3=∠4这两个角是AC与DE被EC所截得到的内错角，可以判定DE∥AC，故选项正确．
    故选：D．

    点评 考查了平行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．阅读下列材料：
    在学习完锐角三角函数后，老师提出一个这样的问题：如图1，在Rt△ABC中，∠ACB=90°，AB=1，∠A=α，求sin2α（用含sinα，cosα的式子表示）．
    聪明的小雯同学是这样考虑的：如图2，取AB的中点O，连接OC，过点C作CD⊥AB于点D，则∠COB=2α，然后利用锐角三角函数在Rt△ABC中表示出AC，BC，在Rt△ACD中表示出CD，则可以求出
    sin2α=$\frac{CD}{OC}$=$\frac{sinα•AC}{{\frac{1}{2}}}$=$\frac{sinα•cosα}{{\frac{1}{2}}}$=2sinα•cosα．
    阅读以上内容，回答下列问题：
    在Rt△ABC中，∠C=90°，AB=1．
    （1）如图3，若BC=$\frac{1}{3}$，则 sinα=$\frac{1}{3}$，sin2α=$\frac{4\sqrt{2}}{9}$；
    （2）请你参考阅读材料中的推导思路，求出tan2α的表达式（用含sinα，cosα的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某地区教育部门为了了解本地九年级学生每周“阳光体育活动”的时间情况，随机调査了本地部分九年级学生，把收集到的数据进行整理并制成了以下两幅统汁图．学生“阳光体育活动”的时间x（h）分为五个等级：A（x≤4），B（4＜x≤6），C（6＜x≤8），D（8＜x≤l0＞，E（x＞10）．
    （1）本次共调查了多少名学生？
    （2）补全条形统计图，扇形统计图中的m=30．
    （3）我们把A，B，C，D，E各等级时间（单位：h）看成：3，5，7，9，11．求被调查学生平均每周的活动时间．
    （4）已知该地九年级学生有8000名，请你估计每周“阳光体育活动”时间大于6h的学生有多少名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．关于x的不等式2x+a≤-3的解集如图所示，则a的取值是（　　）
    A．0B．-1C．-2D．-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

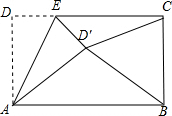    16．如图，矩形ABCD中，AD=5，AB=8，点E为DC上一个动点，把△ADE沿AE折叠，若点D的对应点D′，连接D′B和D′C，以下结论中：
    ①D′B的最小值为3； 
    ②CD′的最小值是$\sqrt{89}-5$
    ③DE=$8-\sqrt{39}$时，△ABD′是直角三角形；
    ④当DE=$\frac{5}{2}$时，△ABD′是等腰三角形．
    其中正确的有（　　）个．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列命题中，是真命题的是（　　）
    ①两条直线被第三条直线所截，同位角相等；
    ②在同一平面内，垂直于同一直线的两条直线互相平行
    ③三角形的三条高中，必有一条在三角形的内部
    ④$\sqrt{-2}$是一个负数．
    A．①②B．②③C．①③D．③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

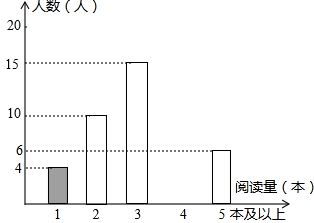    13．某学校为了解学生的课外阅读情况，王老师随机抽查部分学生，并对其暑假期间的课外阅读量进行统计分析，绘制成如图所示但不完整的统计图．已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%，根据所给出信息，解答下列问题：
    （1）求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数；
    （2）将条形统计图补充完整；
    （3）若规定：假期阅读3本及3本以上课外书者为完成假期作业，据此估计该校1500名学生中，完成假期作业的有多少名学生？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算
    （1）|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$
    （2）$\sqrt{3}$（$\sqrt{3}$+$\frac{1}{\sqrt{3}}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，点O是平行四边形ABCD的对角线的交点，则图中全等三角形共有（　　）
    A．4对B．3对C．2对D．1对

    查看答案和解析>>

    同步练习册答案