
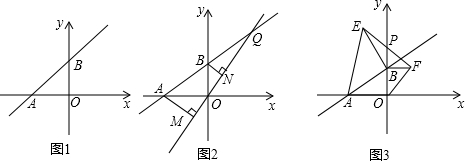
分析 (1)由k=1代入直线l解析式中,求出k,即可得出点A,B坐标,从求出结论;
(2)由OA=OB,利用AAS得到△AMO≌△ONB,用对应线段相等求长度OM,再用勾股定理求出ON即可;
(3)作EG⊥y轴于K点,利用AAS得到△AOB≌△BGE,利用全等三角形对应边相等得到OA=BG,EG=OB,再利用AAS得到△PBF≌△PGE,寻找相等线段,并进行转化,求PB的长,最后用面积公式即可.
解答 解:(1)当k=1时,直线AB解析式为y=2x+6,
∴A(-3,0),B(0,6),
∴OA=3,OB=6,
S△AOB=$\frac{1}{2}$OA×OB=$\frac{1}{2}$×3×6=9,
(2)∵OA=3,
∴OB=OA=3,
∵∠AOB=90°,
∵∠AOM+∠BON=90°,
∵AM⊥OQ,
∴∠AOM+∠OAM=90°,
∴∠OAM=∠BON,
在△AOM和△BON中,$\left\{\begin{array}{l}{∠AMO=∠ONB=90°}\\{∠OAM=∠BON}\\{OA=OB}\end{array}\right.$,
∴△AOM≌△BON,
∴OM=BN=2
,在Rt△BON中,ON=$\sqrt{O{B}^{2}-B{N}^{2}}$=$\sqrt{5}$,
∴MN=OM+ON=2+$\sqrt{5}$
(3)如图3,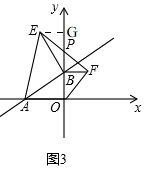
∵直线y=2kx+6k,
∴B(0,6k),
∴OB=6k,
∵△OBF为等腰直角三角形,
∴BF=OB=6k,
作EG⊥y轴于G点,
∵△ABE为等腰直角三角形,
∴AB=BE,∠ABE=90°,
∴∠EBG+∠ABO=90°,
∵∠EBG+∠BEG=90°,
∴∠ABO=∠BEG,
在△AOB和△BKE中,$\left\{\begin{array}{l}{∠BGE=∠AOB=90°}\\{∠ABO=∠BEG}\\{AB=BE}\end{array}\right.$
∴△AOB≌△BGE(AAS),
∴OA=BG,EG=OB=6k,
∵△OBF为等腰直角三角形,
∴OB=BF,
∴EG=BF,
在△EGP和△FBP中,$\left\{\begin{array}{l}{∠EGP=∠PBF=90°}\\{∠GPE=∠BPF}\\{EG=BF}\end{array}\right.$
∴△PBF≌△PGE(AAS),
∴PG=PB,
∴PB=$\frac{1}{2}$BG=$\frac{1}{2}$OA=$\frac{5}{2}$,
∴S=S△BPE+S△BPF=$\frac{1}{2}$BP×EG+$\frac{1}{2}$BP×BF=$\frac{1}{2}$BP×(EG+BF)=$\frac{1}{2}$×$\frac{5}{2}$×(6k+6k)=15k.
点评 此题是三角形综合题,主要考查了待定系数法,全等三角形的判定和性质,勾股定理,等腰直角三角形的性质,解本题的关键是判定△AOM≌△BON,难点是确定出PB的值.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长( )
如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长( )| A. | 4π | B. | 2+4π | C. | 4π-2 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
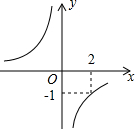 已知函数y与自变量x之间的关系如图所示,那么y与x之间的函数关系式为y=-$\frac{2}{x}$,如果P(-4,c)在这个函数的图象上,那么c值为$\frac{1}{2}$.
已知函数y与自变量x之间的关系如图所示,那么y与x之间的函数关系式为y=-$\frac{2}{x}$,如果P(-4,c)在这个函数的图象上,那么c值为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:填空题
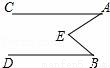
如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com