练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图8-40,是一辆小汽车沿一条高速公路匀速前进的时间t(小时)与速度x(千米/时)关系的图象,根据图象提供的信息回答下列问题:

    图8-40

    (1)这条高速公路的全长是多少千米?

    (2)写出速度与时间之间的函数关系.

    (3)汽车最大速度可以达到多少?

    (4)汽车最慢用几个小时可以到达?如果要在3小时以内到达,汽车的速度应不少于多少?

    答案：300千米.

    提示：以150千米/时行驶了两小时，则路程=150×2=300千米.

    (2)答案：y=.

    提示：由速度=，路程为300千米，则有y=.

    (3)答案：300千米/时.

    提示：据图象用1小时可以行驶完全程，所以汽车最大速度可以达到300千米/时.

    (4)答案：6小时,100千米/时.

    提示：据图象,最低速度为50千米/时，需要6小时行驶完全程.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，甲、乙两辆货车于某日下午2：00同时从A地出发驶往P市，甲车沿一条公路向北偏东60°方向行驶，直达P市，其速度为30公里/小时；乙车先沿一条公路向正东方向行驶半小时后到达B地，卸下部分货物，再沿一条通向东偏北60°方向的公路驶往P市，其速度始终为40公里/小时．
    （1）设出发后经过t小时，甲车与P市的距离为s，求s与t之间的函数关系式，并写出自变量t的取值范围；
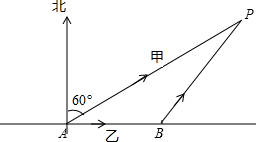    （2）已知在P市新建的移动通讯接收发射塔，其信号覆盖面积可达P市周围方圆30公里的区域（包括边缘地带），除此之外，该地区无其他发射塔，故甲、乙两车司机只能靠P市发射塔进行手机通话联系，问甲、乙两车司机从什么时刻开始可用手机取得联系（精确到分钟）？说明：手机联系必精英家教网须是两人都在信号覆盖范围内方可进行，否则，手机无法联系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

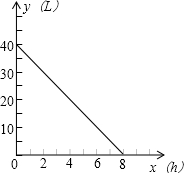    如图是一辆汽车油箱里剩油量y（L）与行驶时间x（h）的图象，则：
    （1）汽车行使前油箱里有
    40
    40
    L汽油．
    （2）油箱中剩油y（L）与行使时间x（h）之间的函数关系是
    y=-5x+40
    y=-5x+40
    ，自变量取值范围为
    0≤x≤8
    0≤x≤8
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图是一辆汽车油箱里剩油量y（L）与行驶时间x（h）的图象，根据图象回答下列问题．
    （1）汽车行使前油箱里有
    40
    40
    L汽油．
    （2）当汽车行使2h，油箱里还有
    30
    30
    L油．
    （3）汽车最多能行使
    8
    8
    h，它每小时耗油
    5
    5
    L．
    （4）油箱中剩油y（L）与行使时间x（h）之间的函数关系是
    y=-5x+40
    y=-5x+40
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图8-40,是一辆小汽车沿一条高速公路匀速前进的时间t(小时)与速度x(千米/时)关系的图象,根据图象提供的信息回答下列问题:

    图8-40

    (1)这条高速公路的全长是多少千米?

    (2)写出速度与时间之间的函数关系.

    (3)汽车最大速度可以达到多少?

    (4)汽车最慢用几个小时可以到达?如果要在3小时以内到达,汽车的速度应不少于多少?

    查看答案和解析>>

    同步练习册答案