
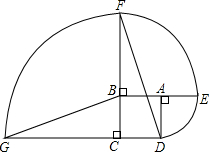
 如图,ABCD是边长为1的正方形,其中
如图,ABCD是边长为1的正方形,其中 |
| DE |
 |
| EF |
 |
| FG |
科目:初中数学 来源: 题型:
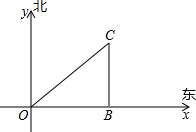 2012年5月“国际保护鲸鱼组织”准备派遣三艘护卫船在南极进行阻止“日本捕鲸船”的“护鲸行动”.在雷达显示图上,标明了三艘护卫船的坐标为O(0,0)、B(40,0)、C(40,30),三艘护卫船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
2012年5月“国际保护鲸鱼组织”准备派遣三艘护卫船在南极进行阻止“日本捕鲸船”的“护鲸行动”.在雷达显示图上,标明了三艘护卫船的坐标为O(0,0)、B(40,0)、C(40,30),三艘护卫船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com