
【题目】下列四个函数中,y的值随着x值的增大而减小的是( )
A.y=2x
B.y=x+1
C.y= ![]() (x>0)
(x>0)
D.y=x2(x>0)
科目:初中数学 来源: 题型:
【题目】学校为表彰在“了不起我的国”演讲比赛中获奖的选手,决定购买甲、乙两种图书作为奖品.已知购买30本甲种图书,50本乙种图书共需1350元;购买50本甲种图书,30本乙种图书共需1450元.
(1)求甲、乙两种图书的单价分别是多少元?
(2)学校要求购买甲、乙两种图书共40本,且甲种图书的数量不少于乙种图书数量的![]() ,请设计最省钱的购书方案.
,请设计最省钱的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.

(1)当t=1s时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当△ACP是等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )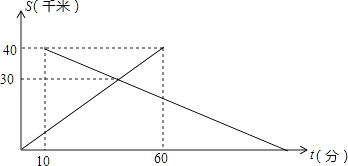
A.14:00
B.14:20
C.14:30
D.14:40
查看答案和解析>>
科目:初中数学 来源: 题型:
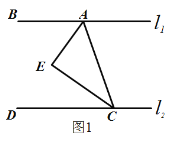
【题目】如图1,点A、B在直线![]() 上,点C、D在直线
上,点C、D在直线![]() 上,AE平分∠BAC,CE平分∠ACD,
上,AE平分∠BAC,CE平分∠ACD,
∠EAC+∠ACE=90° .
(1)请判断![]() 与
与![]() 的位置关系并说明理由;
的位置关系并说明理由;
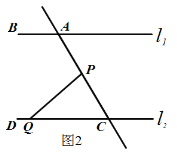
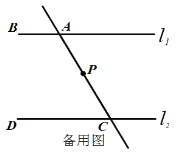
(2)如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图,已知 AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.

解:因为 AB∥CD(已知),
所以∠AGF+ =180°( ),
因为 GH 平分∠AGF,MN 平分∠CMG( ),
所以∠1= ![]() ∠AGF,∠2=
∠AGF,∠2= ![]() ∠CMG( ),
∠CMG( ),
得∠1+∠2=![]() (∠AGF+∠CMG)= ,
(∠AGF+∠CMG)= ,
所以 GH⊥MN( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com