
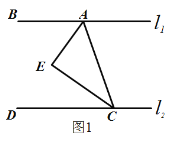
【题目】如图1,点A、B在直线![]() 上,点C、D在直线
上,点C、D在直线![]() 上,AE平分∠BAC,CE平分∠ACD,
上,AE平分∠BAC,CE平分∠ACD,
∠EAC+∠ACE=90° .
(1)请判断![]() 与
与![]() 的位置关系并说明理由;
的位置关系并说明理由;
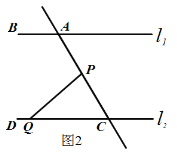
(2)如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.
【答案】(1)![]() ∥
∥![]() ;(2)①当Q在C点左侧时,∠BAC=∠CQP +∠CPQ,②当Q在C点右侧时,∠CPQ+∠CQP+∠BAC=180°.
;(2)①当Q在C点左侧时,∠BAC=∠CQP +∠CPQ,②当Q在C点右侧时,∠CPQ+∠CQP+∠BAC=180°.
【解析】(1)先根据CE平分∠ACD,AE平分∠BAC得出∠BAC=2∠1,∠ACD=2∠2,再由∠1+∠2=90°可知∠BAC+∠ACD=180,故可得出结论;
(2)分两种情况讨论:①当Q在C点左侧时;②当Q在C点右侧时.
(1)![]() ∥
∥![]() .理由如下:
.理由如下:
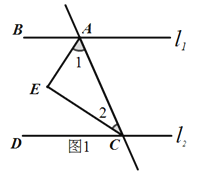
∵AE平分∠BAC,CE平分∠ACD(已知),
∴∠BAC=2∠1,∠ACD=2∠2(角平分线的定义);
又∵∠1+∠2=90°(已知),
∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°(等量代换)
∴![]() ∥
∥![]() (同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(2)①当Q在C点左侧时,过点P作PE∥![]() .
.
∵![]() ∥
∥![]() (已证),
(已证),
∴PE∥![]() (同平行于一条直线的两直线互相平行),
(同平行于一条直线的两直线互相平行),
∴∠1=∠2,(两直线平行,内错角相等),
∠BAC=∠EPC,(两直线平行,同位角相等),
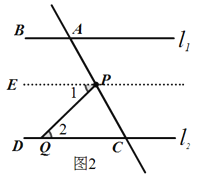
又∵∠EPC=∠1+∠CPQ,
∴∠BAC=∠CQP +∠CPQ(等量代换)
②当Q在C点右侧时,过点P作PE∥![]() .
.
∵![]() ∥
∥![]() (已证),
(已证),
∴PE∥![]() (同平行于一条直线的两直线互相平行),
(同平行于一条直线的两直线互相平行),
∴∠1=∠2,∠BAC=∠APE,(两直线平行,内错角相等),
又∵∠EPC=∠1+
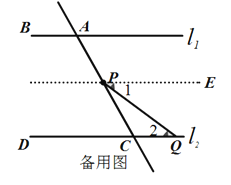
∠APE+∠EPC=180°(平角定义)
∴∠CPQ+∠CQP+∠BAC=180°.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】(14分)盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用![]() (元)及节假日门票费用
(元)及节假日门票费用![]() (元)与游客x(人)之间的函数关系如图所示.
(元)与游客x(人)之间的函数关系如图所示.

(1)a= ,b= ;
(2)直接写出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到红海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程.
(1)x2﹣14x=8(配方法)
(2)x2﹣7x﹣18=0(公式法)
(3)(2x+3)2=4(2x+3)(因式分解法)
(4)2(x﹣3)2=x2﹣9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明上午8点正从家里出发,到书店买书.右图反映了小明买书过程中(从出发到回家)离家的距离y(米)和离家的时间x(分)的关系.
(1)书店离小明家多远?
(2)若小明离开书店返回家时的平均速度比去书店时的平均速度每分钟快15米,问小明几点到家并求小明离开书店后返家过程中y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从全校1200名学生中随机选取一部分学生进行调查,调查情况:A:上网时间 ![]() 小时;B:1小时<上网时间
小时;B:1小时<上网时间 ![]() 小时;C:4小时<上网时间
小时;C:4小时<上网时间 ![]() 小时;D:上网时间>7小时.统计结果制成了如图统计图:
小时;D:上网时间>7小时.统计结果制成了如图统计图:
(1)参加调查的学生有人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由. 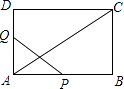
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com