
平面直角坐标系中边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.如图,将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.
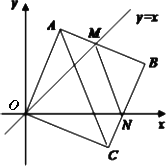
(1)求此时OA旋转的度数;
(2)旋转过程中,当MN与AC平行时,求正方形OABC旋转的度数;
(3)设△MBN的周长为p,在正方形OABC旋转的过程中,p值是否有变化?请证明你的结论.
|
解:延长BA交 (1)∵直线 ∴∠MOE=∠MON= ∴A点第一次落在直线y=x上时停止旋转时,OA旋转了45°;(2分) (2)∵四边形ABCO是正方形 ∴∠B=∠OAB=∠OCB=∠AOC=90°,OA=OC, 且∠BAC=∠BCA=45° ∵MN∥AC,∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45° ∠BMN=∠BNM.∴BM=BN.(4分) 又∵BA=BC, ∴BA-BM=BC-BN 即AM=CN. 又∵∠OAM=∠OCN=90°,OA=OC, ∴△OAM≌△OCN.(6分) ∴∠AOM=∠CON. ∴∠AOM=∠CON= = ∴当MN和AC平行时,正方形OABC旋转的度数为22.5°(7分) (3) ∵由旋转的性质得:∠AOE=∠CON.(8分) 又∵∠OAE+∠OAB=180°,∠OAB=90° ∴∠OAE=90° ∴∠OAE=∠OCN=90°, 又∵OA=OC ∴△OAE≌△OCN.(9分) ∴OE=ON,AE=CN 又∵∠MOE=∠MON=45°, OM=OM, ∴△OME≌△OMN,(10分) ∴MN=ME=AM+AE. ∴MN=AM+CN. ∴ ∴在正方形OABC旋转的过程中
|


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
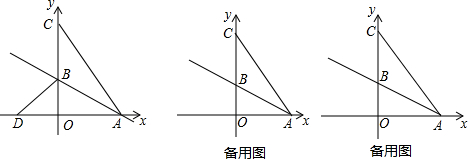
 在如图所示的平面直角坐标系中,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的三个顶点的坐标为:A(1,6)、B(2,2)、C(6,3).
在如图所示的平面直角坐标系中,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的三个顶点的坐标为:A(1,6)、B(2,2)、C(6,3).查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
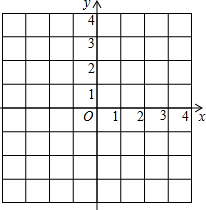 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com