
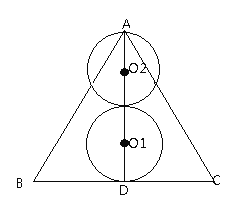
【题目】已知等边△ABC边长为2,D为BC中点,连接AD.点O在线段AD上运动(不含端点A、D),以点O为圆心,![]() 长为半径作圆,当
长为半径作圆,当![]() O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
【答案】![]() 或
或![]()
【解析】
根据题意作图,根据![]() O与△ABC的边有且只有两个公共点时得到两种情况,分别讨论求解即可.
O与△ABC的边有且只有两个公共点时得到两种情况,分别讨论求解即可.
∵![]() O与△ABC的边有且只有两个公共点
O与△ABC的边有且只有两个公共点
∴①当圆O与BC相交于两点时,
如图,点圆O1与BC相切时,恰好有一个交点,此时,O1D=![]() ,
,
故当![]() 时,
时,![]() O与△ABC的边有且只有两个公共点;
O与△ABC的边有且只有两个公共点;
②当圆O与△ABC的AB、AC各交于一点时,
∵等边△ABC边长为2,D为BC中点
∴∠B=∠BAC=60°,AD为△ABC的高、中线、∠BAC的角平分线,
∴BD=1,则AD=![]()
如图,圆O2与△交于3点,此时AO2=![]() ,
,
则O2D=![]() -
-![]() =
=![]()
∵![]() O与△ABC的边有且只有两个公共点,则点A在圆O内部,
O与△ABC的边有且只有两个公共点,则点A在圆O内部,
∴当![]() 时,
时,![]() O与△ABC的边有且只有两个公共点;
O与△ABC的边有且只有两个公共点;
综上,当![]() 或
或![]() 时,
时,![]() O与△ABC的边有且只有两个公共点.
O与△ABC的边有且只有两个公共点.
故填:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图(1)所示.图(2)建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系是![]() .请回答下列问题:
.请回答下列问题:

(1)柱子OA的高度是多少米?
(2)喷出的水流距水平面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池外?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点A(﹣1,0)和点B(3,0),且有最小值为﹣2.
(1)求这个函数的解析式;
(2)函数的开口方向、对称轴;
(3)当y>0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
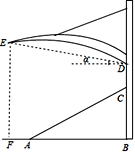
求:(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程.原计划每天拆迁![]() ,因为准备工作不足,第一天少拆迁了
,因为准备工作不足,第一天少拆迁了![]() .从第二天开始,该工程队加快了拆迁速度,第三天拆迁了
.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了![]() .求:
.求:
![]() 该工程队第一天拆迁的面积;
该工程队第一天拆迁的面积;
![]() 若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
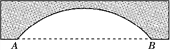
【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
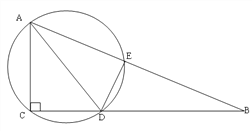
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE。
(1)求证:AC=AE;
(2)求△ACD外接圆的直径。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com