
 已知:如图,△ABC的角平分线BE、CF相交于点P.求证:点P在∠A的平分线上.
已知:如图,△ABC的角平分线BE、CF相交于点P.求证:点P在∠A的平分线上.  口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
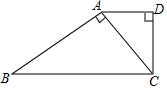 如图,已知直角梯形ABCD中,AD∥BC,∠D=90°,∠B=30°,CD=9$\sqrt{3}$,对角线CA⊥AB,求AD和BC的长度.
如图,已知直角梯形ABCD中,AD∥BC,∠D=90°,∠B=30°,CD=9$\sqrt{3}$,对角线CA⊥AB,求AD和BC的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
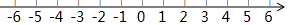 在数轴上画出表示下列各数的点,并用“<”号将这些数按从小到大的顺序连接起来:
在数轴上画出表示下列各数的点,并用“<”号将这些数按从小到大的顺序连接起来:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知a、b、c在数轴上的位置如图所示,试化简|a+b|-|b|+|b+c|+|c|的结果是( )
已知a、b、c在数轴上的位置如图所示,试化简|a+b|-|b|+|b+c|+|c|的结果是( )| A. | a+b | B. | a+b-2c | C. | -a-b-2c | D. | a+b+2c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 用一段长30米的篱笆围成一个一边靠墙的矩形花圃,墙长为18米,另三边用篱笆恰好围成.围成的花圃是如图的矩形ABCD.设AB边的长为x米,花圃ABCD的面积为S平方米,则S与x之间的函数关系式是s=x(30-2x).(不必写出自变量取值范围)
用一段长30米的篱笆围成一个一边靠墙的矩形花圃,墙长为18米,另三边用篱笆恰好围成.围成的花圃是如图的矩形ABCD.设AB边的长为x米,花圃ABCD的面积为S平方米,则S与x之间的函数关系式是s=x(30-2x).(不必写出自变量取值范围)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com