
 如图,AB、CD是两栋楼,且AB=CD=30m,两楼间距AC=24m,当太阳光与水平线的夹角为30°时,AB楼在CD楼上的影子是
如图,AB、CD是两栋楼,且AB=CD=30m,两楼间距AC=24m,当太阳光与水平线的夹角为30°时,AB楼在CD楼上的影子是科目:初中数学 来源: 题型:
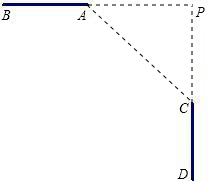 在A、C两点处分别与道路相切),测得AC=60米,∠ACP=45度.
在A、C两点处分别与道路相切),测得AC=60米,∠ACP=45度.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB、CD是两条高速公路,M、N是两个村庄,现建造一个货物中转站,要求到AB、CD的距离相等,且到两个村庄的距离也相等.(不写作法,保留作图痕迹)
如图,AB、CD是两条高速公路,M、N是两个村庄,现建造一个货物中转站,要求到AB、CD的距离相等,且到两个村庄的距离也相等.(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:AB和CD是两堵和地面BC垂直的墙,两堵墙之间的距离是14米,一个10米长的梯子下端支在地面上某点,上端靠在墙上.
如图:AB和CD是两堵和地面BC垂直的墙,两堵墙之间的距离是14米,一个10米长的梯子下端支在地面上某点,上端靠在墙上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com