
分析 (1)先利用平方差公式和完全平方公式计算,进一步合并得出答案即可;
(2)利用整式的乘法计算,进一步合并即可;
(3)先利用积的乘方计算,再利用单项式的乘法计算方法计算即可;
(4)先利用平方差公式计算,再利用完全平方公式计算即可;
(5)利用完全平方公式计算,进一步合并,再算除法即可;
(6)先算0指数幂,负指数幂与乘方,再算加减.
解答 解:(1)原式=4a2-9b2-a2+6ab-9b2
=3a2+6ab-18b2;
(2)原式=x2-xy-2x2+xy+y2
=-x2+y2;
(3)x4y2•(-x9y6)
=-x13y8;
(4)原式=(2x+y)2-9z2
=4x2+4xy+y2-9z2;
(5)原式=[x2+2xy+y2-x2+2xy-y2]÷(2xy)
=4xy÷(2xy)
=2;
(6)原式=1-8-64
=-71.
点评 此题考查整式的混合运算,掌握运算顺序与计算方法是解决问题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | a<-1 | B. | a>$\frac{3}{2}$ | C. | -$\frac{3}{2}$<a<1 | D. | -1<a<$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
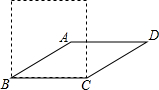 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
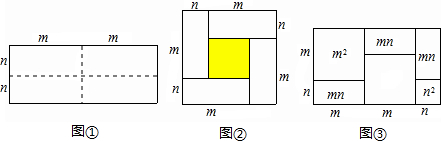
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B.
如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com