
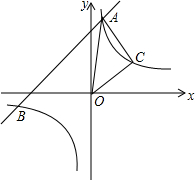
 如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B.
如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B.分析 (1)先把A点坐标代入 y1=$\frac{m}{x}$求出m,从而得到反比例函数解析式;再把A点和C点坐标分别代入y2=kx+b得关于k、b的方程组,然后解方程组求出k和b,于是可得到一次函数解析式;
(2)根据反比例函数与一次函数的交点问题,通过方程组$\left\{\begin{array}{l}{y=\frac{3}{2}x+4}\\{y=-\frac{2}{x}}\end{array}\right.$得B(-$\frac{2}{3}$,3),然后根据函数图象,找出反比例函数图象在一次函数图象上方所对应的自变量的范围即可.
解答 解:(1)把A(-2,1)代入 y1=$\frac{m}{x}$得m=-2×1=-2,所以反比例函数解析式为y1=-$\frac{2}{x}$;
把A(-2,1)、C(0,4)分别代入y2=kx+b得$\left\{\begin{array}{l}{-2k+b=1}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=4}\end{array}\right.$,
所以一次函数解析式为y2=$\frac{3}{2}$x+4;
(2)解方程组$\left\{\begin{array}{l}{y=\frac{3}{2}x+4}\\{y=-\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{2}{3}}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,则B(-$\frac{2}{3}$,3),
所以当x<-2或-$\frac{2}{3}$<x<0时,反比例函数值大于一次函数值.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间/分 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
| 速度/(千米/时) |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$.其中正确的是①②④(写出所有正确结论的序号).
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$.其中正确的是①②④(写出所有正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3).反比例函数y1=$\frac{k}{x}$图象经过点C,一次函数y2=ax+b的图象经过点A、C
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3).反比例函数y1=$\frac{k}{x}$图象经过点C,一次函数y2=ax+b的图象经过点A、C查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com