
| 4 |
| 5 |
| AE |
| EC |
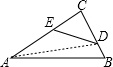 解:连接AD,设△ABD、△ACD、△ADE、△CDE的面积分别为s1、s2、s3、s4,
解:连接AD,设△ABD、△ACD、△ADE、△CDE的面积分别为s1、s2、s3、s4,| s1 |
| s2 |
| BD |
| CD |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 5 |
| 4 |
| 5 |
| 7 |
| 15 |
| 3 |
| 15 |
| s3 |
| s4 |
| AE |
| CE |
| ||
|
| 7 |
| 3 |
| 1 |
| 5 |
| 3h |
| 5 |
| h |
| x |
| AE+EC |
| EC |
| AE |
| EC |
| 2 |
| 3 |
| 7 |
| 3 |
| 2 |
| 3 |


科目:初中数学 来源: 题型:
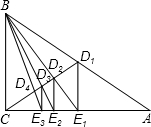 已知:如图,在Rt△ABC中,点D1是斜边AB的中点,过点D1作D1E1⊥AC于点E1,连接BE1交CD1于点D2;过点D2作D2E2⊥AC于点E2,连接BE2交CD1于点D3;过点D3作D3E3⊥AC于点E3,如此继续,可以依次得到点D4、D5、…、Dn,分别记△BD1E1、△BD2E2、△BD3E3、…、△BDnEn的面积为S1、S2、S3、…Sn.设△ABC的面积是1,则S1=
已知:如图,在Rt△ABC中,点D1是斜边AB的中点,过点D1作D1E1⊥AC于点E1,连接BE1交CD1于点D2;过点D2作D2E2⊥AC于点E2,连接BE2交CD1于点D3;过点D3作D3E3⊥AC于点E3,如此继续,可以依次得到点D4、D5、…、Dn,分别记△BD1E1、△BD2E2、△BD3E3、…、△BDnEn的面积为S1、S2、S3、…Sn.设△ABC的面积是1,则S1=查看答案和解析>>
科目:初中数学 来源:2003年全国初中数学竞赛(天津赛区)初赛试卷(解析版) 题型:填空题
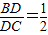 ,若在边AC上取一点,使四边形ABDE的面积为
,若在边AC上取一点,使四边形ABDE的面积为 ,则
,则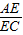 的值为 .
的值为 .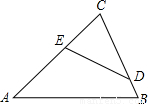
查看答案和解析>>
科目:初中数学 来源:2010年福建省龙岩市长汀县河田二中保送生数学模拟试卷(解析版) 题型:填空题
 ,则
,则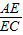 的值为 .
的值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com