
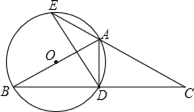
【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
【答案】(1)证明见解析;(2)⊙O的半径为![]() ;(3)AE=
;(3)AE=![]() .
.
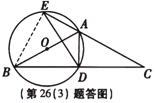
【解析】试题分析:(1)根据直径所对的圆周角是直角得到AD⊥BC,应用等腰三角形的三线合一证得点D为BC的中点;
(2)应用等腰三角形的性质和判定证得BD=DE=3,进而求得BD=3,AD=1,应用勾股定理求得AB的长,即可得到半径的长;
(3)解法一:通过证明△CAB∽△CDE,应用相似三角形的性质解得CE的长,再求AE的长;
解法二:连接BE,通过证明△ADC∽△BEC,解得CE的长,再求AE的长.
试题解析:(1)证明:∵AB为⊙O的直径,
∴AD⊥BC,
又∵AB=AC,
∴D是BC的中点.
(2)解:∵AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠C=∠E,则DC=DE,
∴BD=DE=3,
又BD-AD=2,
∴AD=1,
在Rt△ABD中,BD=3,AD=1,
∴AB=![]() ,
,
则⊙O的半径为![]() .
.
(3)解法一:在△CAB和△CDE中,
∠B=∠E,∠C=∠C(公共角),
∴△CAB∽△CDE,
∴![]() ,
,
∵CA=AB=![]() ,
,
∴![]() ,
,
∴AE=CE-AC=![]() =
=![]() .
.
解法二:连接BE,
∵AB为⊙O的直径,
∴∠BEC=![]() ,
,
在△ADC和△BEC中,
∠ADC=∠BEC=![]() ,∠C=∠C,
,∠C=∠C,
∴△ADC∽△BEC,
∴![]() ,
,
∴![]() ,
,
∴AE=CE-AC=![]() =
=![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
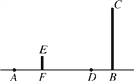
【题目】如图,在一座大厦(图中BC所示)前面30m的地面上,有一盏地灯A照射大厦,身高为1.6m的小亮(图中EF所示)站在大厦和灯之间,若小亮从现在所处位置径直走向大厦,当他走到距离大厦只有5m的D处时停下.
(1)请在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC上的影子;
(2)请你求出此时小亮的影长.
查看答案和解析>>
科目:初中数学 来源: 题型:
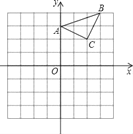
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生拓展视野、丰富知识,加深与自然和文化的亲近感,增加对集体生活方式和社会公共道德的体验,我区某中学决定组织部分师生去随州炎帝故里开展研学旅行活动.在参加此次活动的师生中,若每位老师带![]() 个学生,还剩
个学生,还剩![]() 个学生没人带;若每位老师带
个学生没人带;若每位老师带![]() 个学生,就有一位老师少带
个学生,就有一位老师少带![]() 个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有
个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有![]() 名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.

(1)参加此次研学旅行活动的老师有 人;学生有 人;租用客车总数为 辆;
(2)设租用![]() 辆乙种客车,租车费用为
辆乙种客车,租车费用为![]() 元,请写出
元,请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过![]() 元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1.
(2)点C1的坐标为( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2![]() .
.
①若∠C=30°,求图中阴影部分的面积;
②若![]() ,求BE的长.
,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
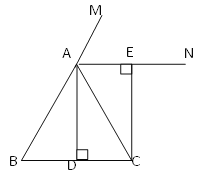
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com