练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

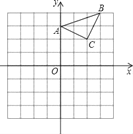
    【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

    （1）以点B为位似中心，在网格内画出△A1B1C1，使△A1B1C1与△ABC位似，且位似比为2：1．

    （2）点C1的坐标为（　 　，　 　）．

    【答案】(1)见解析；（2）(1,0)

    【解析】试题分析：延长BA到A1，使BA1=2BA，则点A1为点A的对应点，同样方法得到C点的对应点C1，点B1与B点重合，则可得到△A1B1C1；

    （2）由（1）中的图形即可写出点C1的坐标.

    试题解析：（1）如图，△A1B1C1为所作；

    （2）由图可得，C1点的坐标为（1，0）．

    故答案为：（1，0）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

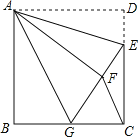
    【题目】如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：

    ①△ABG≌△AFG；② BG=GC；③ AG∥CF；④∠GAE=45°．

    则正确结论的个数有( )

    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

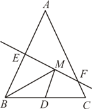
    【题目】如图，等腰三角形ABC的底边BC的长为4，面积是12，腰AB的垂直平分线EF分别交AB、AC于点E、F，若点D为底边BC的中点，点M为线段EF上一动点，则△BDM的周长的最小值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

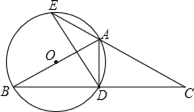
    【题目】如图，△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD、DE．

    （1）求证：D是BC的中点；

    （2）若DE=3，BD﹣AD=2，求⊙O的半径；

    （3）在（2）的条件下，求弦AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2+2（m﹣1）x+m2﹣4=0有两个不相等的实数根．

    （1）求m的取值范围；

    （2）若m为正整数，且该方程的两个根都是整数，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

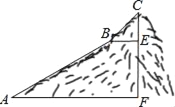
    【题目】如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．

    （1）求AB段山坡的高度EF；

    （2）求山峰的高度CF（结果保留根式）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

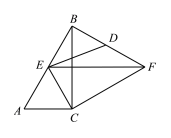
    【题目】如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=4，△ABC绕点C顺时针旋转得△CEF，当E落在AB边上时，连接BF，取BF的中点D，连接ED，则ED的长是( )

    A.2B.4C.6D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

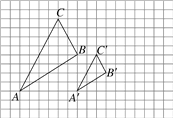
    【题目】如图，△ABC与△A′B′C′是以点O为位似中心的位似图形，它们的顶点都在正方形网格的格点上．

    (1)画出位似中心O；

    (2)△ABC与△A′B′C′的相似比为__________，面积比为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

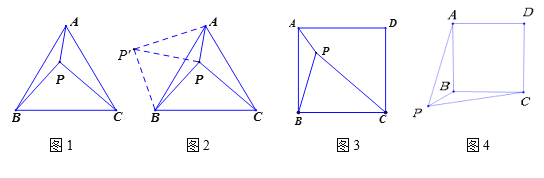
    【题目】（问题提出）在数学“共生课堂”上，某合作小组提出了这样一个问题：如图1，在等边三角形ABC内有一点P，且PA＝1，PB＝2，PC＝．你能求出∠APB的度数吗？

    （问题解决）（1）李清同学分析题目后，发现以PA、PB、PC的长为边的三角形是直角三角形，他找到了正确的思路：如图2，将△BPC绕点B逆时针旋转60°，得到△BP′A．连接PP′，易得△P′PB是等边三角形，△P′PA是直角三角形，则得∠BPP′＝_________，∠APB＝_________．

    （问题类比）（2）同组的祁响同学突然想起曾经解决过的一个问题：如图3，点P是正方形ABCD内一点，PA=1，PB=2，PC=3．求∠APB的度数．请你写出解答过程．

    （问题延伸）（3）夏老师留了一个思考题：如图4，若点P是正方形ABCD外一点，PA=，PB=1，PC=．则∠APB的度数．请你写出解答过程．

    查看答案和解析>>

    同步练习册答案