
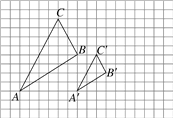
【题目】如图,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
(1)画出位似中心O;
(2)△ABC与△A′B′C′的相似比为__________,面积比为__________.
科目:初中数学 来源: 题型:
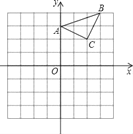
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1.
(2)点C1的坐标为( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2![]() .
.
①若∠C=30°,求图中阴影部分的面积;
②若![]() ,求BE的长.
,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明某天上午9时骑自行车离开家,15时回家,他离家的距离与时间的变化情况如图所示.

(1)10时时他离家 ![]() ,他到达离家最远的地方时是 时,此时离家
,他到达离家最远的地方时是 时,此时离家 ![]() ;
;
(2)他可能在哪段时间内休息,并吃午餐?
(3)他在出行途中,哪段时间内骑车速度最快,速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
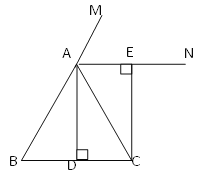
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=﹣x+2与x轴、y轴分别交于A、B两点,直线BC交x轴负半轴于点C,∠BCA=30°,如图①.
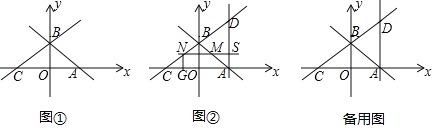
(1)求直线BC的解析式.
(2)在图①中,过点A作x轴的垂线交直线CB于点D,若动点M从点A出发,沿射线AB方向以每秒![]() 个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
(3)若点M是直线AB在第二象限上的一点,点N、P分别在直线BC、直线AD上,是否存在以M、B、N、P为顶点的四边形是菱形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com