
����Ŀ����ͼ����֪������y=![]() x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
��1���������ߵĽ���ʽ����2������P����y��ƽ�е�ֱ��l��ֱ��AB��AC�ֱ��ڵ�E��F�����ı���AECP��������ʱ�����P�����ꣻ
��3������PΪ�����ߵĶ���ʱ����ֱ��AC���Ƿ���ڵ�Q��ʹ����C��P��QΪ���������������ABC���ƣ������ڣ������Q�����꣬�������ڣ���˵�����ɣ�

���𰸡���1��y= ![]() x2+2x+1��2��P����
x2+2x+1��2��P����![]() ����
����![]() ����3��Q����4��1����3��1��
����3��Q����4��1����3��1��
�������������������1���ô���ϵ������������߽���ʽ���ɣ�
��2�����P��m�� ![]() m2+2m+1������ʾ��PE=��
m2+2m+1������ʾ��PE=��![]() m2��3m������S������AECP=S��AEC+S��APC=
m2��3m������S������AECP=S��AEC+S��APC=![]() AC��PE������������ϵʽ�������ֵ���ɣ�
AC��PE������������ϵʽ�������ֵ���ɣ�
��3�����жϳ�PF=CF���ٵõ���PCF=��EAF����C��P��QΪ���������������ABC���ƣ�������������㼴�ɣ�
�����������1������A��0��1����B����9��10�����������ϣ�
��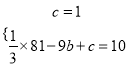 ��
��
��![]() ��
��
�������ߵĽ���ʽΪy=![]() x2+2x+1��
x2+2x+1��
��2����AC��x�ᣬA��0��1��
��![]() x2+2x+1=1��
x2+2x+1=1��
��x1=��6��x2=0��
����C�����꣨��6��1����
����A��0��1����B����9��10����
��ֱ��AB�Ľ���ʽΪy=��x+1��
���P��m�� ![]() m2+2m+1��
m2+2m+1��
��E��m����m+1��
��PE=��m+1����![]() m2+2m+1��=��
m2+2m+1��=��![]() m2��3m��
m2��3m��
��AC��EP��AC=6��
��S������AECP=S��AEC+S��APC=![]() AC��EF+
AC��EF+![]() AC��PF
AC��PF
=![]() AC����EF+PF��
AC����EF+PF��
=![]() AC��PE
AC��PE
=![]() ��6������
��6������![]() m2��3m��
m2��3m��
=��m2��9m
=����m+![]() ��2+
��2+![]() ��
��
����6��m��0
����m=��![]() ʱ���ı���AECP����������ֵ��
ʱ���ı���AECP����������ֵ��![]() ����ʱ��P����
����ʱ��P����![]() ����
����![]() ����
����
��3����y=![]() x2+2x+1=
x2+2x+1=![]() ��x+3��2��2��
��x+3��2��2��
��P����3����2����
��PF=yF��yP=3��CF=xF��xC=3��
��PF=CF��
���PCF=45��
ͬ���ɵã���EAF=45����
���PCF=��EAF��
����ֱ��AC�ϴ�������������Q��
��Q��t��1����AB=9![]() ��AC=6��CP=3
��AC=6��CP=3![]()
����C��P��QΪ���������������ABC���ƣ�
������CPQ�ס�ABCʱ��
��![]() ��
��
��![]() ��
��
��t=��4��
��Q����4��1��
������CQP�ס�ABCʱ��
��![]() ��
��
��![]() ��
��
��t=3��
��Q��3��1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ʵ����У�Сǿ��A�س������ر�ƫ��60��ķ����н�3 ![]() ǧ����B�أ�Ȼ�����ر�ƫ��30�㷽���н���3ǧ����Ŀ�ĵ�C��
ǧ����B�أ�Ȼ�����ر�ƫ��30�㷽���н���3ǧ����Ŀ�ĵ�C�� 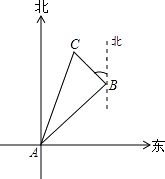
��1����A��C����֮��ľ��룻
��2����ȷ��Ŀ�ĵ�C�ڵ�A��ʲô����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ���ڣ���P��Բ�ϵĵ��������Ϊ7����С����Ϊ1�����Բ�İ뾶Ϊ( )
A. 6B. 4C. 3D. 4��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��C��AB��һ�㣬��D��E�ֱ���AB���࣬AD��BE����AD=BC��BE=AC�� 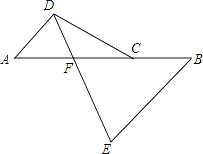
��1����֤��CD=CE��
��2������DE����AB�ڵ�F�������BEF����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�У�AD��BC��DEƽ�֡�ADB����BDC=��C������ABD��ƽ������CD���ӳ��߽���F���ҡ�F=x��������0��x��90�������ABC=�㣬���ú���x��ʽ�ӱ�ʾ�� 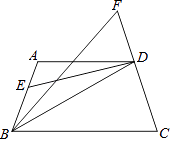
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC��AE=AF��BE��CF���ڵ�D����������н��ۣ��١�ABE�ա�ACF���ڡ�BDF�ա�CDE����D�ڡ�BAC��ƽ�����ϣ�������ȷ���ǣ� �� 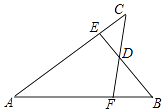
A.��
B.��
C.�ٺ͢�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��8a2b+2��2a2b��3ab2����3��4a2b��ab2��������a=��2��b=3��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com