练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在一次实践活动中，小强从A地出发，沿北偏东60°的方向行进3 千米到达B地，然后再沿北偏西30°方向行进了3千米到达目的地C．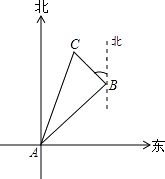
    （1）求A、C两地之间的距离；
    （2）试确定目的地C在点A的什么方向？

    【答案】
    （1）解：过B作BD⊥AD，垂足为D，

    ∵∠BAD=30°，∠ABD=60°，

    ∴∠CBA=90°

    在Rt△ABC中，AB=3 km，BC=3km．

    ∴AC=6km


    （2）解：由（1）可知， = =sin∠CAB，

    ∴∠CAB=30°，

    ∴点C在A的北偏东30°方向上．


    【解析】（1）过B作BD⊥AD，根据已知得到∠CBA=90°，已知其它两边的长，从而利用勾股定理求得AC的长．（2）根据三角函数可以得到∠CAB的度数，从而确定C的位置．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，两块相同的三角板完全重合在一起，∠A=30°，AC=10，把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置，点C′在AC上，A′C′与AB相交于点D，则C′D= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小惠在纸上画了一条数轴后，折叠纸面，使数轴上表示1的点与表示﹣3的点重合，若数轴上A，B两点之间的距离为2014（A在B的左侧），且A，B两点经上述折叠后重合，则A点表示的数为（ ）
    A.﹣1006
    B.﹣1007
    C.﹣1008
    D.﹣1009

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BCAD=AE2；④∠DFE=2∠DAC ;⑤若连接CH，则CH∥EF.其中正确的个数为（ ）

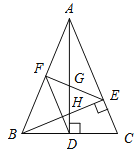
    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2+2x+m=0的有两个相等的实数根，则m为（ ）
    A.2
    B.﹣2
    C.1
    D.﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1 ， A2 ， A3 ， A4 ， …表示，则顶点A55的坐标是（ ）

    A.（13，13）
    B.（﹣13，﹣13）
    C.（14，14）
    D.（﹣14，﹣14）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列式子从左到右的变形是因式分解的是(　　)

    A. a2＋4a－21＝a(a＋4)－21

    B. (a－3)(a＋7)＝a2＋4a－21

    C. a2＋4a－21＝(a－3)(a＋7)

    D. a2＋4a－21＝(a＋2)2－25

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．

    （1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

    （3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(本小题满分8分) 如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC（精确到0.1米）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）

    查看答案和解析>>

    同步练习册答案