
【题目】如图△ABC 中,AC=BC,∠ACB=120°,点 D 在线段 AB 上运动(D 不与 A、B 重合),连接 CD,作∠CDE=30°,DE 交 BC 于点 E,若△CDE 是等腰三角形,则∠ADC 的度数是___________.

【答案】60°或105°
【解析】
分类讨论:当CD=DE时;当DE=CE时;当EC=CD时;然后利用等腰三角形的性质和三角形的内角和定理进行计算.
△CDE可以是等腰三角形,
∵△CDE是等腰三角形;
①当CD=DE时,
∵∠CDE=30°,
∴∠DCE=∠DEC=75°,
∴∠ADC=∠B+∠DCE=105°,
②当DE=CE时,∵∠CDE=30°,
∴∠DCE=∠CDE=30°,
∴∠ADC=∠DCE+∠B=60°.
③当EC=CD时,
∠BCD=180°∠CED∠CDE=180°30°30°=120°
∵∠ACB=180°∠A∠B=120°,
∴此时,点D与点A重合,不合题意.
综上,△ADC可以是等腰三角形,此时∠ADC的度数为60°或105°.
故答案为60°或105°.


科目:初中数学 来源: 题型:
【题目】长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )

A. 7![]() B.
B. ![]()
C. 24D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )

A. 1 m B. 2 m C. 3 m D. 6 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:
![]() 如图
如图![]() 等边
等边![]() 内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求
内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求![]() 的度数.为了解决本题,我们可以将
的度数.为了解决本题,我们可以将![]() 绕顶点A旋转到
绕顶点A旋转到![]() 处,此时
处,此时![]() ≌
≌![]() ,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出
,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出![]() ______;
______;
![]() 基本运用
基本运用
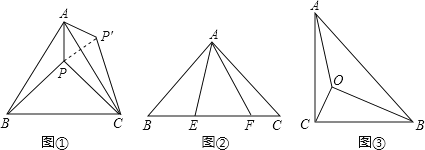
请你利用第![]() 题的解答思想方法,解答下面问题:已知如图
题的解答思想方法,解答下面问题:已知如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,E、F为BC上的点且
,E、F为BC上的点且![]() ,求证:
,求证:![]() ;
;
![]() 能力提升
能力提升
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O为
,点O为![]() 内一点,连接AO,BO,CO,且
内一点,连接AO,BO,CO,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.

(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=60°,∠ACB=50°,延长CB至点D,使DB=BA,延长BC至点E,使CE=CA,连接AD,AE. 求∠DAE的度数
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
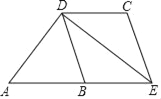
【题目】如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
(1)求证:四边形BDCE是菱形;
(2)若AD=8,BD=6,求菱形BDCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com