
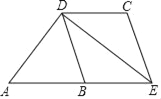
【题目】如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
(1)求证:四边形BDCE是菱形;
(2)若AD=8,BD=6,求菱形BDCE的面积.
科目:初中数学 来源: 题型:
【题目】如图△ABC 中,AC=BC,∠ACB=120°,点 D 在线段 AB 上运动(D 不与 A、B 重合),连接 CD,作∠CDE=30°,DE 交 BC 于点 E,若△CDE 是等腰三角形,则∠ADC 的度数是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c (a≠0)上.

(1)求抛物线的解析式.
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个交点D,求m的值及点D的坐标.
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,若∠ACB=∠DBC,则不能证明两个三角形全等的条件是( )

A.∠ABC=∠DCBB.∠A=∠DC.AB=DCD.AC=DB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,过B作⊙O的切线,在该切线上取点C,连接AC交⊙O于D,若⊙O的半径是6,∠C=36°,则劣弧AD的长是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 3π
D. 3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海南建省30年来,各项事业取得令人瞩目的成就,以2016年为例,全省社会固定资产总投资约3730亿元,其中包括中央项目、省属项目、地(市)属项目、县(市)属项目和其他项目.图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图,请完成下列问题:
(1)在图1中,先计算地(市)属项目投资额为 亿元,然后将条形统计图补充完整;
(2)在图2中,县(市)属项目部分所占百分比为m%、对应的圆心角为β,则m= ,β= 度(m、β均取整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是Rt△ABC斜边BC上的高.
(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);
(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;
(3)在(2)的条件下,连结DEDH.求证:ED⊥HD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com