
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.

【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)由等腰直角三角形的性质得出AB=BC,BD=BE,∠ABC=∠DBE=90°,得出∠ABD=CBE,证出△ABD≌△CBE(SAS),得出AD=CE;
(2)△ABD≌△CBE得出∠BAD=∠BCE,再由∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,得出∠AFC=∠ABC=90°,证出结论.
(1)证明:∵△ABC和△DBE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=CBE,
在△ABD和△CBE中,
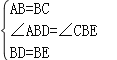 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE;
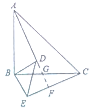
(2)延长AD分别交BC和CE于G和F,如图所示:
∵△ABD≌△CBE,
∴∠BAD=∠BCE,
∵∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,
又∵∠BGA=∠CGF,
∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.


科目:初中数学 来源: 题型:
【题目】我县某楼盘准备以每平方米6500元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米5265元的均价开盘销售,则每次下调的百分率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
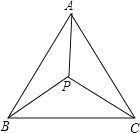
【题目】如图5,点P在正△ABC内一点,∠APB=125°, ∠BPC=100°,则以AP,BP,CP为边长的三角形各内角的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知关于x的一元二次方程x2﹣2x﹣k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≥1B. k>1C. k≥﹣1D. k>﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 必然事件发生的概率为1 B. 不可能事件发生的概率为0
C. 随机事件发生的概率大于等于0、小于等于1 D. 概率很小的事件不可能发生
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com