
����Ŀ�����Ͻ�ʡ30������������ҵȡ��������Ŀ�ijɾͣ���2016��Ϊ����ȫʡ���̶��ʲ���Ͷ��Լ3730��Ԫ�����а���������Ŀ��ʡ����Ŀ���أ��У�����Ŀ���أ��У�����Ŀ��������Ŀ��ͼ1��ͼ2�ֱ����������Ŀ��Ͷ�ʶ����������ͳ��ͼ������ͳ��ͼ��������������⣺
��1����ͼ1�У��ȼ���أ��У�����ĿͶ�ʶ�Ϊ�� ����Ԫ��Ȼ������ͳ��ͼ����������
��2����ͼ2�У��أ��У�����Ŀ������ռ�ٷֱ�Ϊm%����Ӧ��Բ�Ľ�Ϊ������m=�� ������=�� ���ȣ�m������ȡ��������

���𰸡���1��830��������ͳ��ͼ������������������2��18��65.
��������
��1����ȫʡ���̶��ʲ���Ͷ��Լ3730��Ԫ��ȥ������Ŀ��Ͷ�ʼ�����õأ��У�����ĿͶ�ʶ�Ӷ���ȫͼ����
��2�����أ��У�����ĿͶ�ʳ�����Ͷ�����m��ֵ������360�ȳ����أ��У�����ĿͶ�ʶ���ռ�����ɵã�
�⣺��1���أ��У�����ĿͶ�ʶ�Ϊ3730����200+530+670+1500��=830����Ԫ����
��ȫͼ�����£�

�ʴ�Ϊ��830��
��2�����У�����Ŀ������ռ�ٷֱ�Ϊm%=![]() ��100%��18%����m=18��
��100%��18%����m=18��
��Ӧ��Բ�Ľ�Ϊ��=360���![]() ��65�㣬
��65�㣬
�ʴ�Ϊ��18��65��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
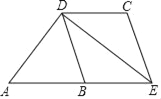
����Ŀ����ͼ����ABC�У���ABC=60������ACB=50�����ӳ�CB����D��ʹDB=BA���ӳ�BC����E��ʹCE=CA������AD��AE. ���DAE�Ķ���
 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ADE�У���ADE=90������B��AE���е㣬����D��DC��AE��DC=AB������BD��CE��
��1����֤���ı���BDCE�����Σ�
��2����AD=8��BD=6��������BDCE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B����O�����㣬��OAB��ǵ�ƽ���߽���O����һ��C��CD��AB��AB���ӳ�����D��
��1����֤��CD����O�����ߣ�
��2��EΪ![]() ���е㣬FΪ��O��һ�㣬EF��AB��G����tan��AFE=
���е㣬FΪ��O��һ�㣬EF��AB��G����tan��AFE=![]() ��BE=BG��EG=3
��BE=BG��EG=3![]() ������O�İ뾶��
������O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC�У���C=90������A=30����AB���е�D��BC�߾���Ϊ3 cm������AC���ҵ�E��ʹBE+EDֵ��С����BE+ED����Сֵ��________cm.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��DΪ��ABC�ı�AB���ӳ�����һ�㣬��D��DF��AC������ΪF����BC��E,��BD=BE,��֤����ABC�ǵ���������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�ǵȱ������Σ�PΪƽ���ڵ�һ�����㣬BP=BA��0<��PBC<180 ��DBƽ�֡�PBC����DB=DA��

��1����BP��BA�غ�ʱ����ͼ1�������BPD�Ķ�����
��2����BP�ڡ�ABC���ڲ�ʱ(��ͼ2)�����BPD�Ķ�����
��3����BP�ڡ�ABC���ⲿʱ������ֱ��д����BPD�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ɱ߳���Ϊ1����λ���ȵ�С��������ɵ������У������˸���ABC�͡�DEF������ Ϊ�����ߵĽ��㣩���Լ���������ֱ��m��
��1��������ABC����ֱ��m�ԳƵġ�A1B1C1��
��2������DEF������ƽ��5����λ���ȣ�������ƽ��4����λ���ȣ�����ƽ�ƺ�õ��ġ�D1E1F1��
��3�����A+��E= ________�㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���֪��BAC��45����AD��BC��D���ֱ���AB��ACΪ�Գ��ᣬ������ABD����ACD����Գ�ͼ�Σ�D��ĶԳƵ�ΪE��F���ӳ�EB��FC�ཻ��G�㣬�õ�������AEGF(AE��EG��GF��AF,![]() ��EAF����E����F����G=90��)��
��EAF����E����F����G=90��)��

(1) ��AD��6��BD��2����CG�ij���
(2) ��BG��a,CG��b,BC��c.
��AE=_______.(��a��b��c��ʾ)
�����������������֤���ɶ���![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com