
【题目】△ABC是等边三角形,P为平面内的一个动点,BP=BA,0<∠PBC<180 ,DB平分∠PBC,且DB=DA.

(1)当BP与BA重合时(如图1),求∠BPD的度数;
(2)当BP在∠ABC的内部时(如图2),求∠BPD的度数;
(3)当BP在∠ABC的外部时,请你直接写出∠BPD的度数.
【答案】(1)30°;(2)30°;(3)∠BPD=30°或150°.
【解析】
(1)由于P,A重合,DP=DB,∠DBP=∠DPB,因为DB是∠PBC的平分线,因此,∠DBP=∠DPB=30°;
(2)连接CD,BP=BC,BD又是∠PBC的平分线,则△PBD≌△CBD,有∠BPD=∠BCD,那么关键是求∠BCD的值,可通过证明△ACD和△BCD全等来得出,∠BCD=∠ACD=30°,然后求出∠BPD的度数;
(3)同(2)的证法完全一样,先求出∠BCD的度数,然后证明△BPD≌△BCD.(当∠BPD是钝角时,∠BPD=∠BCD=(360-60)÷2=150°,还是用的(2)中的△BPD≌△BCD,△BCD≌△ACD).
解:(1)在等边三角形ABC中,
∴∠ABC=∠PBC=60°,
∵DB平分∠PBC,
∴∠PBD=30°
∵DB=DA,
∴∠DBP=∠DPB=30°;
(2)如图,连接CD,
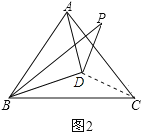
∵点D在∠PBC的平分线上
∴∠PBD=∠CBD
∵△ABC是等边三角形
∴BA=BC=AC,∠ACB=60°
∵BP=BA
∴BP=BC
∵BD=BD
∴△PBD≌△CBD(SAS)
∴∠BPD=∠BCD
∵DB=DA,BC=AC,CD=CD
∴△BCD≌△ACD
∴∠BCD=∠ACD=![]() ∠ACB=30°
∠ACB=30°
∴∠BPD=30°;
(3)当BP在∠ABC的外部时,如图
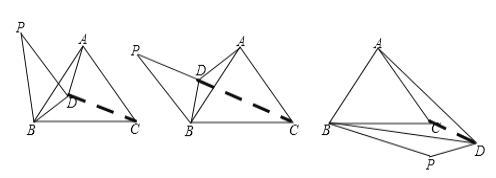
当∠BPD是锐角时,由(2)知,△BCD≌△ACD
∴∠BCD=∠ACD=![]() ∠ACB=30°,
∠ACB=30°,
由△PBD≌△CBD,
∴∠BPD=30°;
当∠BPD是钝角时,由(2)知,△BCD≌△ACD
∴∠BCD=∠ACD,
∴∠BCD=(360°-60°)÷2=150°,
由△PBD≌△CBD,
∴∠BPD=∠BCD=150°;
综合上述,∠BPD=30°或150°.


科目:初中数学 来源: 题型:
【题目】作图题(1)如图1,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线l成轴对称的△AB′C′;
②在直线l上找一点P,使PB+PC的长最短.

(2)利用网格(图2)作图,请你先在图中的BC边上找一点P,使点P到边AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() ,点
,点![]() 分别在
分别在![]() 轴正半轴和负半轴上,
轴正半轴和负半轴上,![]() .
.
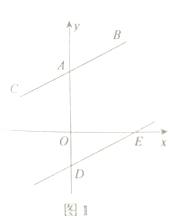
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)在![]() 和
和![]() 内作射线
内作射线![]() ,
,![]() ,分别与过
,分别与过![]() 点的直线交于第一象限内的点
点的直线交于第一象限内的点![]() 和第三象限内的点
和第三象限内的点![]() .
.
①如图2,若![]() ,
,![]() 恰好分别平分
恰好分别平分![]() 和
和![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,当
,当![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
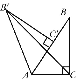
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,Rt△AB'C'可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段B'C的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com