
【题目】如图,已知在![]() 中,
中,![]() ,点D沿BC自B向C运动
,点D沿BC自B向C运动![]() 点D与点B、C不重合
点D与点B、C不重合![]() ,作
,作![]() 于E,
于E,![]() 于F,则
于F,则![]() 的值
的值![]()
![]()

A. 不变 B. 增大 C. 减小 D. 先变大再变小
【答案】C
【解析】
现根据BE⊥AD于E,CF⊥AD于F,可证明CF∥BE,
根据直线平行的性质可得:∠DCF=∠DBF,然后设CD=a,DB=b,∠DCF=∠DBE=α,
利用三角函数定义可得:CF=DCcosα,BE=DBcosα,
继而可得:BE+CF=(DB+DC)cosα=BCcosα,再根据余弦函数的性质可得:
在O<α<90°,当点D从B→D运动时,α是逐渐增大的,cosα的值是逐渐减小的,
继而可得BE+CF=BCcosα的值是逐渐减小的.
∵BE⊥AD于E,CF⊥AD于F,
∴CF∥BE,
∴∠DCF=∠DBF,
设CD=a,DB=b,∠DCF=∠DBE=α,
∴CF=DCcosα,BE=DBcosα,
∴BE+CF=(DB+DC)cosα=BCcosα,
∵∠ABC=90°,
∴O<α<90°,
当点D从B→D运动时,α是逐渐增大的,
∴cosα的值是逐渐减小的,
∴BE+CF=BCcosα的值是逐渐减小的.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对于一元二次方程ax2+bx+c=0 (a≠0),下列说法中错误的是( )
A. 当a>0,c<0时,方程一定有实数根
B. 当c=0时,方程至少有一个根为0
C. 当a>0,b=0,c<0时,方程的两根一定互为相反数
D. 当abc<0时,方程的两个根同号,当abc>0时,方程的两个根异号
查看答案和解析>>
科目:初中数学 来源: 题型:
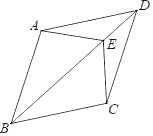
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果∠BDC=30°,DE=2,EC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,P为平面内的一个动点,BP=BA,0<∠PBC<180 ,DB平分∠PBC,且DB=DA.

(1)当BP与BA重合时(如图1),求∠BPD的度数;
(2)当BP在∠ABC的内部时(如图2),求∠BPD的度数;
(3)当BP在∠ABC的外部时,请你直接写出∠BPD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.

(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党中央“下好一盘棋,共护一江水”的号召,某治污公司决定购买甲、乙两种型号的污水处理设备共10台.经调查发现:购买一台甲型设备比购买一台乙型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元,且一台甲型设备每月可处理污水240吨,一台乙型设备每月可处理污水200吨.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少万元?
(2)若治污公司购买污水处理设备的资金不超过109万元,月处理污水量不低于2080吨.
①求该治污公司有几种购买方案;
②如果为了节约资金,请为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CPQ是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为______cm/s时,在某一时刻也能够使△BPD与△CPQ全等.
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都按逆时针方向沿△ABC的三边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在△ABC的哪条边上?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com